Apache Hadoop Wordcount Example
In this example, we will demonstrate the Word Count example in Hadoop. Word count is the basic example to understand the Hadoop MapReduce paradigm in which we count the number of instances of each word in an input file and gives the list of words and the number of instances of the particular word as an output.
1. Introduction
Hadoop is an Apache Software Foundation project which is the open source equivalent of Google MapReduce and Google File System. It is designed for distributed processing of large data sets across a cluster of systems running on commodity standard hardware.
Hadoop is designed with an assumption that hardware failure is a norm rather an exception. All hardware fails sooner or later and the system should be robust and capable enough to handle the hardware failures gracefully.
2. MapReduce
Apache Hadoop consists of two core components, one being Hadoop Distributed File System(HDFS) and second is the Framework and APIs for MapReduce jobs.
In this example, we are going to demonstrate the second component of Hadoop framework called MapReduce. If you are interested in understanding the basics if HDFS, the article Apache Hadoop Distributed File System Explained may be of help. Before moving to the example of MapReduce paradigm, we shall understand what MapReduce actually is.
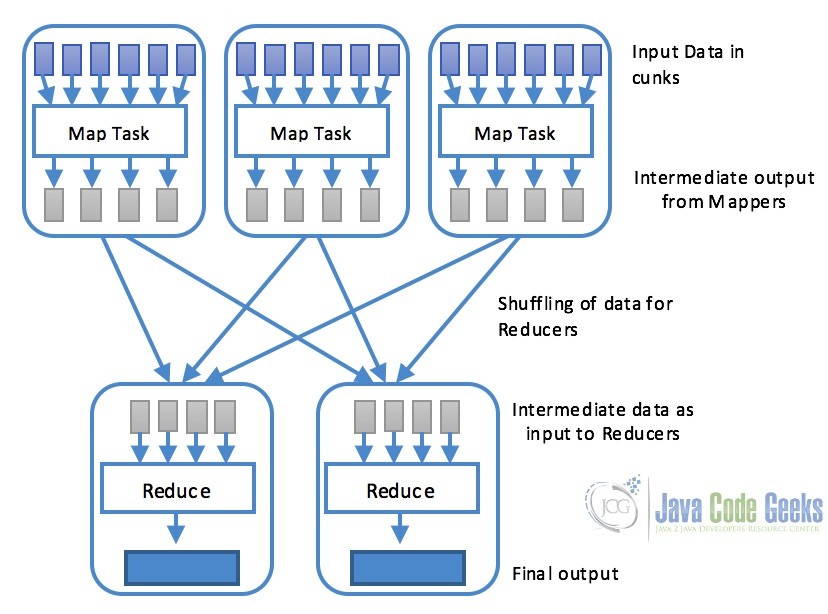
MapReduce is basically a software framework or programming paradigm, which enable users to write programs as separate components so that data can be processed parallelly across multiple systems in a cluster. MapReduce consists of two parts Map and Reduce.
-
Map: Map task is performed using a
map()function that basically performs filtering and sorting. This part is responsible for processing one or more chunks of data and producing the output results which are generally referred as intermediate results. As shown in the diagram below, map task is generally processed in parallel provided the mapping operation is independent of each other. -
Reduce: Reduce task is performed by
reduce()function and performs a summary operation. It is responsible for consolidating the results produced by each of the Map task.
3. Word-Count Example
Word count program is the basic code which is used to understand the working of the MapReduce programming paradigm. The program consists of MapReduce job that counts the number of occurrences of each word in a file. This job consists of two parts map and reduce. The Map task maps the data in the file and counts each word in data chunk provided to the map function. The outcome of this task is passed to reduce task which combines and reduces the data to output the final result.
3.1 Setup
We shall use Maven to setup a new project for Hadoop word count example. Setup a maven project in Eclipse and add the following Hadoop dependency to the pom.xml. This will make sure we have the required access to the Hadoop core library.
<dependency>
<groupId>org.apache.hadoop</groupId>
<artifactId>hadoop-core</artifactId>
<version>1.2.1</version>
</dependency>
After adding the dependency, we are ready to write our word count code.
3.2 Mapper Code
The mapper task is responsible for tokenizing the input text based on space and create a list of words, then traverse over all the tokens and emit a key-value pair of each word with a count of one. Following is the MapClass:
package com.javacodegeeks.examples.wordcount;
import java.io.IOException;
import java.util.StringTokenizer;
import org.apache.hadoop.io.IntWritable;
import org.apache.hadoop.io.LongWritable;
import org.apache.hadoop.io.Text;
import org.apache.hadoop.mapreduce.Mapper;
public class MapClass extends Mapper{
private final static IntWritable one = new IntWritable(1);
private Text word = new Text();
@Override
protected void map(LongWritable key, Text value,
Context context)
throws IOException, InterruptedException {
//Get the text and tokenize the word using space as separator.
String line = value.toString();
StringTokenizer st = new StringTokenizer(line," ");
//For each token aka word, write a key value pair with
//word and 1 as value to context
while(st.hasMoreTokens()){
word.set(st.nextToken());
context.write(word,one);
}
}
}
Following is what exactly map task does:
- Line 13-14, defines static variable
onewith interger value 1 andwordfor storing the words. - Line 22-23, In
mapmethod the inputTextvaroable is converted toStringand Tokenized based on the space to get all the words in the input text. - Line 27-30, For each word in the text, set the
wordvariable and pass a key-value pair ofwordand integer valueoneto thecontext.
3.3 Reducer Code
Following code snippet contains ReduceClass which extends the MapReduce Reducer class and overwrites the reduce() function. This function is called after the map method and receives keys from the map() function corresponding to the specific key. Reduce method iterates over the values, adds them and reduces to a single value before finally writing the word and the number of occurrences of the word to the output file.
package com.javacodegeeks.examples.wordcount;
import java.io.IOException;
import java.util.Iterator;
import org.apache.hadoop.io.IntWritable;
import org.apache.hadoop.io.Text;
import org.apache.hadoop.mapreduce.Reducer;
public class ReduceClass extends Reducer{
@Override
protected void reduce(Text key, Iterable values,
Context context)
throws IOException, InterruptedException {
int sum = 0;
Iterator valuesIt = values.iterator();
//For each key value pair, get the value and adds to the sum
//to get the total occurances of a word
while(valuesIt.hasNext()){
sum = sum + valuesIt.next().get();
}
//Writes the word and total occurances as key-value pair to the context
context.write(key, new IntWritable(sum));
}
}
Following is the workflow of reduce function:
- Lines 17-18, define a variable
sumas interger with value 0 andIteratorover the values received by the reducer. - Lines 22-24, Iterate over all the values and add the occurances of the words in
sum - Line 27, write the
wordand thesumas key-value pair in thecontext
3.4 The Driver Class
So now when we have our map and reduce classes ready, it is time to put it all together as a single job which is done in a class called driver class. This class contains the main() method to setup and run the job.
package com.javacodegeeks.examples.wordcount;
import org.apache.hadoop.conf.Configured;
import org.apache.hadoop.fs.Path;
import org.apache.hadoop.io.IntWritable;
import org.apache.hadoop.io.Text;
import org.apache.hadoop.mapreduce.Job;
import org.apache.hadoop.mapreduce.lib.input.FileInputFormat;
import org.apache.hadoop.mapreduce.lib.output.FileOutputFormat;
import org.apache.hadoop.mapreduce.lib.output.TextOutputFormat;
import org.apache.hadoop.util.Tool;
import org.apache.hadoop.util.ToolRunner;
public class WordCount extends Configured implements Tool{
public static void main(String[] args) throws Exception{
int exitCode = ToolRunner.run(new WordCount(), args);
System.exit(exitCode);
}
public int run(String[] args) throws Exception {
if (args.length != 2) {
System.err.printf("Usage: %s needs two arguments, input and output
files\n", getClass().getSimpleName());
return -1;
}
//Create a new Jar and set the driver class(this class) as the main class of jar
Job job = new Job();
job.setJarByClass(WordCount.class);
job.setJobName("WordCounter");
//Set the input and the output path from the arguments
FileInputFormat.addInputPath(job, new Path(args[0]));
FileOutputFormat.setOutputPath(job, new Path(args[1]));
job.setOutputKeyClass(Text.class);
job.setOutputValueClass(IntWritable.class);
job.setOutputFormatClass(TextOutputFormat.class);
//Set the map and reduce classes in the job
job.setMapperClass(MapClass.class);
job.setReducerClass(ReduceClass.class);
//Run the job and wait for its completion
int returnValue = job.waitForCompletion(true) ? 0:1;
if(job.isSuccessful()) {
System.out.println("Job was successful");
} else if(!job.isSuccessful()) {
System.out.println("Job was not successful");
}
return returnValue;
}
}
Following is the workflow of main function:
- Line 22-26, check if the required number of arguments are provided.
- Line 29-31, create a new
Job, set the name of the job and the main class. - Line 34-35, set the input and the output paths from the arguments.
- Line 37-39, set the key value type classes and the output format class. These classes need to be the same type whichw e use in the map and reduce for the output.
- Line 42-43, set the Map and Reduce classes in the
job - Line 46, execute the job and wait for its completion
4. Code Execution
There are two ways to execute the code we have written, first is to execute it within Eclipse IDE itself for the testing purpose and second is to execute in the Hadoop Cluster. We will see both ways in this section.
4.1 In Eclipse IDE
For executing the wordcount code in eclipse. First of all, create an input.txt file with dummy data. For the testing purpose, We have created a file with the following text in the project root.
This is the example text file for word count example also knows as hello world example of the Hadoop ecosystem. This example is written for the examples article of java code geek The quick brown fox jumps over the lazy dog. The above line is one of the most famous lines which contains all the english language alphabets.
In Eclipse, Pass the input file and output file name in the project arguments. Following is how the arguments looks like. In this case, the input file is in the root of the project that is why just filename is required, but if your input file is in some other location, you should provide the complete path.
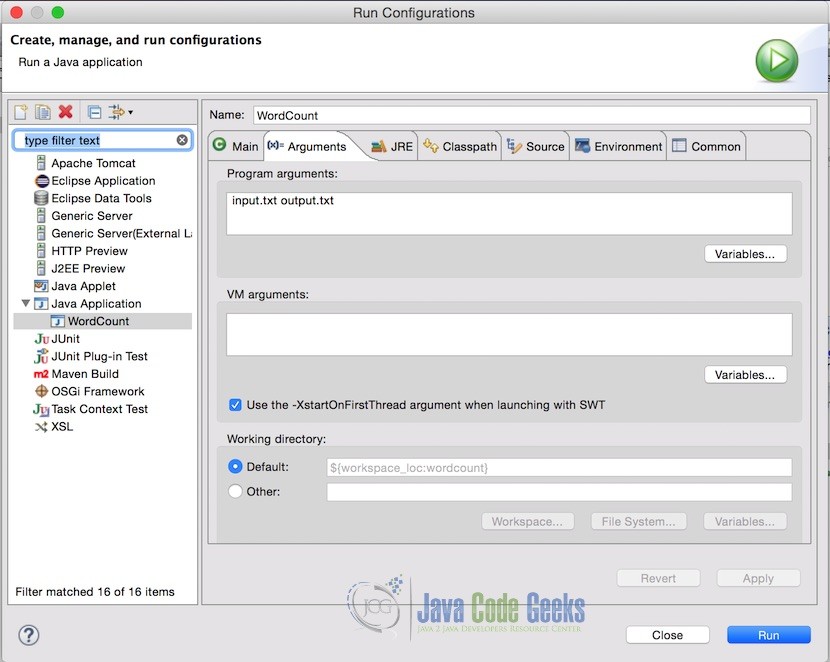
Note: Make sure the output file does not exist already. If it does, the program will throw an error.
After setting the arguments, simply run the application. Once the application is successfully completed, console will show the output.
Below is the content of the output file:
Hadoop 1 The 2 This 2 above 1 all 1 alphabets. 1 also 1 article 1 as 1 brown 1 code 1 contains 1 count 1 dog. 1 ecosystem. 1 english 1 example 4 examples 1 famous 1 file 1 for 2 fox 1 geek 1 hello 1 is 3 java 1 jumps 1 knows 1 language 1 lazy 1 line 1 lines 1 most 1 of 3 one 1 over 1 quick 1 text 1 the 6 which 1 word 1 world 1 written 1
4.2 On Hadoop Cluster
For running the Wordcount example on hadoop cluster, we assume:
- Hadoop cluster is setup and running
- Input file is at the path
/user/root/wordcount/Input.txtin the HDFS
In case, you need any help with setting up the hadoop cluster or Hadoop File System, please refer to the following articles:
- How to Install Apache Hadoop on Ubuntu
- Apache Hadoop Cluster Setup Example(with Virtual Machines)
- Apache Hadoop Distributed File System Explained
- Apache Hadoop FS Commands Example
Now, first of all make sure the Input.txt file is present at the path /user/root/wordcount using the command:
hadoop fs -ls /user/root/wordcount
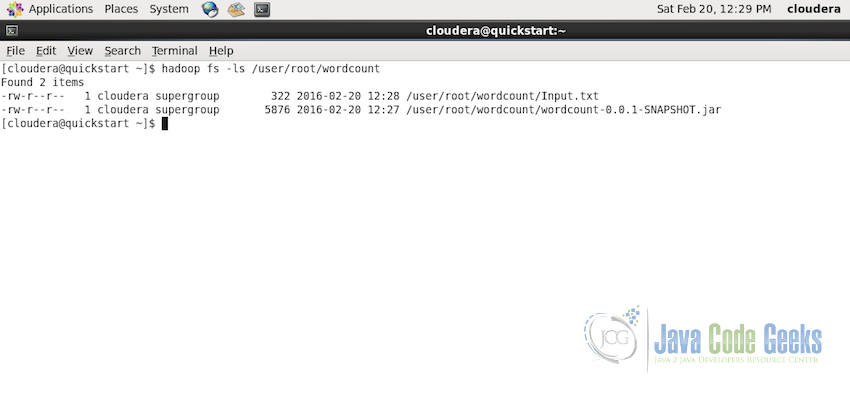
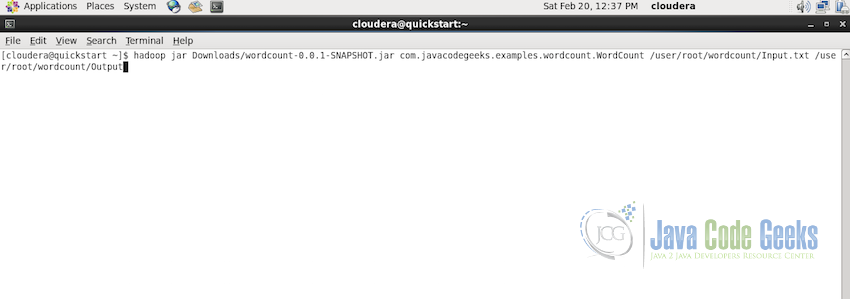
Now it is time to submit the MapReduce job. Use the following command for execution
hadoop jar Downloads/wordcount-0.0.1-SNAPSHOT.jar com.javacodegeeks.examples.wordcount.Wordcount /user/root/wordcount/Input.txt /user/root/wordcount/Output
In the above code, jar file is in the Downloads folder and the Main class is at the path com.javacodegeeks.examples.wordcount.Wordcount
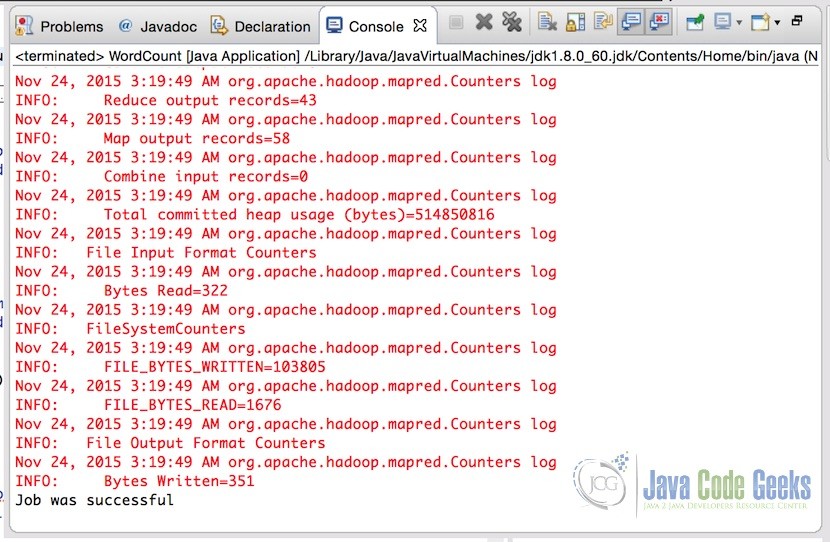
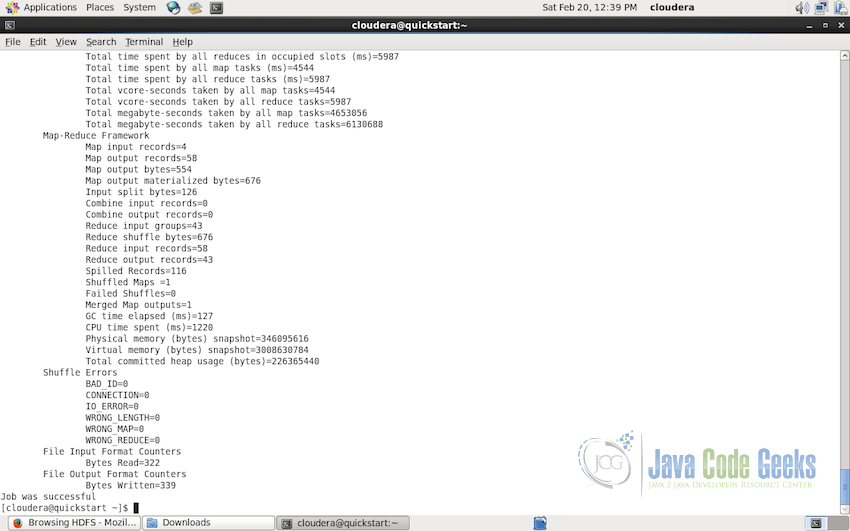
Following should be the output of the execution. Console output’s last line informs us that the job was successfully completed.
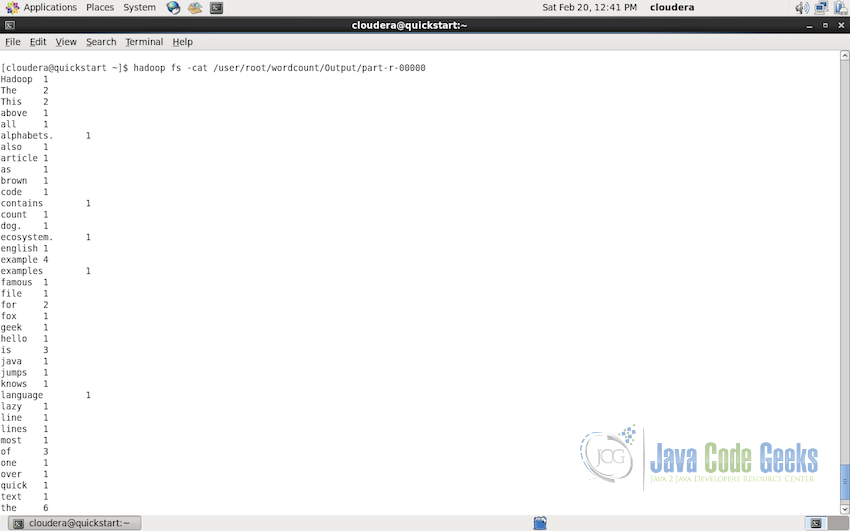
Now we can read the output of the Wordcount map reduce job in the folder /user/root/wordcount/Output/. Use the following command to check the output in the console:
hadoop fs -cat /user/root/wordcount/Output/part-r-00000
Following screenshot display the content of the Output folder on the console.
5. Conclusion
This example explains the MapReduce paradigm with respect to Apache Hadoop and how to write the word count example in MapReduce step by step. Next we saw how to execute the example in the eclipse for the testing purpose and also how to execute in the Hadoop cluster using HDFS for the input files. The article also provides links to the other useful articles for setting up Hadoop on Ubuntu, Setting up Hadoop Cluster, Understanding HDFS and Basic FS commands. We hope, this article serves the best purpose of explaining the basics of the Hadoop MapReduce and provides you with the solid base for understanding Apache Hadoop and MapReduce.
6. Download the Eclipse Project
Click on the following link to download the complete eclipse project of wordcount example.
You can download the full source code of this example here: HadoopWordCount




how do we get word count by ascending order