Topological Sort Java Example
In this article, we will discuss the Topological sort Java algorithm. We will start with graphs, some common types, and to store graphs.
1. Graph and common types
A graph is a non-linear data structure consisting of a finite set of Vertices (also called nodes) connected by Edges.
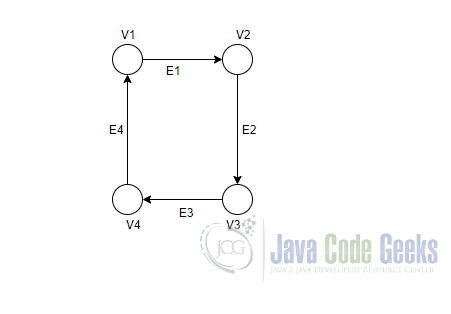
In the above example, the graph has vertices V1, V2, V3, V4 with edges E1, E2, E3, E4. Let us look at some classification of graphs
Graphs can be classified as below
- Directed or Undirected
- Weighted or Unweighted
- Cyclic or Acyclic
Directed or Undirected: Directed graphs have edges pointed from one node to another, whereas Undirected graphs do not have any directions.
Weighted or Unweighted: A graph is said to be weighted if it has weight (this could be to indicate either distance or time taken between locations, where each node represents a location) mentioned on the edges.
Cyclic or Acyclic: A graph is said to be cyclic if it contains a cycle (a cycle in a graph is a non-empty trail in which only repeated vertices are the first and last vertices)
2. Store a graph
Topological sort algorithms for graphs can be stored as:
- Edge list
- Adjacency matrix
- Adjacency list
Let us take an example of an undirected graph with 5 vertices and 6 edges to discuss these types. An index is also indicated beside each edge.
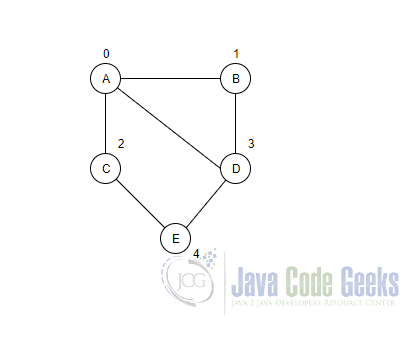
Edge list: This deals with storing the vertices and edges as a list. So, in our example, it can be represented as {(0,1), (0,2), (0,3), (1,3), (2,4), (3,4)}. As it’s an undirected graph, edge (0,1) is the same as (1,0). Hence (1,0) is not mentioned in the above list. We can note that the time and space complexity, in this case, would be O(E), where E represents Edges.
Adjacency Matrix: This deals with storing the edges between nodes as a matrix representation.
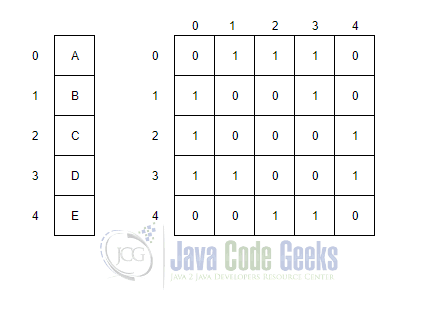
In this representation, the index of all vertices is indicated in a matrix format with values 0 and 1, with 1 representing an edge between two vertices. The graph, in this case, would be represented as {(0,1,1,1,0) , (1,0,0,1,0) , (1,0,0,0,1) , (1,1,0,0,1) ,(0,0,1,1,0)}. We can note that time complexity, in this case, would be O(V) and space complexity would be O(V2), where V represents the number of vertices. This representation would be more useful when the graph is dense (i.e. too many edges)
Adjacency List: In this case, the graph is represented as a list, with the index indicating the vertex/ node and the value at that index representing its neighbors. In our example, it can be shown as {(1,2,3) , (0,3) , (0,4) , (0,1,4) , (2,3)}. We can note that space is saved in this representation and is better for sparse graphs (i.e too few edges). Time complexity would be O(V) and space complexity would be O(E), where E and V represent the number of Edges and Vertices.
3. Topological Sort Java example
A Topological sort can work only for directed acyclic graphs (DAG). Let us look at an example to discuss topological sort in java. We will use a similar example as previous but as a directed one.
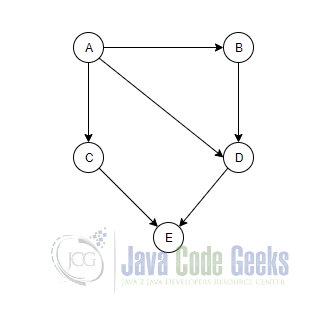
The above directed acyclic graph contains 5 nodes and 6 edges. We will use the adjacency list representation as the graph is sparse.
The nodes are {A, B, C, D, E}, and edges are {(A,B) , (A,C) , (A,D) , (B,D) , (C,E),(D,E)}. The sort should always start from the node that does not have any incoming directed edges (Node A in this case). The visited node list at this moment would be {A}. The neighbor nodes for A are B, C, and D. The next neighbor node that can be visited is either C or B. D has another incoming directed edge from an unvisited node (B), so cant be visited at this point. Let us visit C. The visited node list would now be {A, C}. The neighbor node for C is E, but can’t be visited as it has another incoming directed edge from an unvisited node (D). So, let us take up the next neighbor node for A i.e. B. The visited node list would now be {A, C, B}. B’s neighbor node D can also be visited as it no longer has any directed edges from unvisited nodes, thereby making the visited list to {A, C, B, D}. Finally, we can visit the last node E making the visited list as {A, C, B, D, E} and this would be our sorted order. Note that this is not the only solution. {A, B, D, C, E} is also acceptable.
When implementing this algorithm programmatically, we shall use Stack, HashMap, and ArrayList. We’ll implement this recursively, and hence the last visited node would be the first on the stack. After all the nodes are visited, we will have our topological sort in the stack in reverse order.
Graph.java
import java.util.List;
import java.util.Stack;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Iterator;
/*
* Graph class holds nodes and their edges.
* The class also contains the logic to sort
*/
public class Graph{
// a list to hold all the edges for each node/ vertex
private HashMap<Character, ArrayList> edges;
// a list of hold all the nodes
private List nodes;
// a list to indicate nodes that were visited/ traversed
private List nodeVisited;
// a list to hold all the edges
private ArrayList edgeList;
// a public constructor to set the nodes and intialize edge list
public Graph(List vertices){
nodes = vertices;
edges = new HashMap();
nodeVisited = new ArrayList();
}
// method to add edge to a node. i.e. adding edges for given nodes.
public void addEdge(Character x, Character y){
// If the node (key) and edge (value) are being added for first time
if(!edges.containsKey(x)){
edgeList = new ArrayList();
} else {
// if the node already has edges added
edgeList = edges.get(x);
}
edgeList.add(y);
edges.put(x,edgeList);
}
// method containing the logic to sort the given nodes recursively
public void topologicalSort(){
Stack stack = new Stack();
// iterate through all the nodes and their neighbours if not already visited.
for (Character c : nodes){
if(!nodeVisited.contains(c)){
sort(c, stack);
}
}
// print all the elements in the stack in reverse order
while(!stack.empty()){
System.out.print(stack.pop()+ " ");
}
}
// this recursive method iterates through all the nodes and neighbours.
// Pushes the visited items to stack
public void sort(Character ch, Stack stack){
// add the visited node to list, so we don't repeat this node again
nodeVisited.add(ch);
// the leaf nodes wouldn't have neighbors. A check added to avoid null pointer
if(edges.get(ch)!=null){
// get all the neighbor nodes , by referring its edges
Iterator iter = edges.get(ch).iterator();
Character neighborNode;
// if an edge exists for the node, then visit that neighbor node
while(iter.hasNext()){
neighborNode = iter.next();
if(!nodeVisited.contains(neighborNode)){
sort(neighborNode,stack);
}
}
}
// push the latest node on to the stack
stack.push(new Character(ch));
}
}
TopologicalSort.java
import java.util.ArrayList;
import java.util.Arrays;
public class TopologicalSort{
public static void main(String args[]){
// define the array with nodes
ArrayList list = new ArrayList(Arrays.asList('A','B','C','D','E'));
// defining the edges for nodes
Graph charGraph = new Graph(list);
charGraph.addEdge('A','B');
charGraph.addEdge('A','C');
charGraph.addEdge('A','D');
charGraph.addEdge('B','D');
charGraph.addEdge('C','E');
charGraph.addEdge('D','E');
charGraph.topologicalSort();
}
}
The output of the above code would be {A C B D E}.
These were the topological sort algorithms.
4. Download source code
You can download the full source code of this example here: Topological Sort Java Example


