Min Heap Java Example
In this article, we will explain what Min Heap is in Java using examples. We shall discuss Heap Data Structure and its implementation in Java.
1. Introduction
Heap is a binary tree-based data structure. Now let us understand each word in this sentence in greater detail.
Tree:- A tree is a hierarchy-based data structure, you have a certain order in placing the elements.
Binary Tree:- A binary tree has a parent with at most two nodes or children.
Data Structure:- Data Structures are responsible for holding or storing the data inside a program. Ex:- Arrays, Lists, Heap, Stack, Queue, etc.
Heap -: Heap is a balanced binary tree data structure where a root node is compared with its children and arranged accordingly. Based on its arrangement, Heap is divided into two types:-
- Min Heap:- A Heap in which, the value in each internal node is smaller than or equal to the values in the children of that node.
- Max Heap:- A Heap in which, the value in each internal node is greater than or equal to the values in the children of that node.
2. Min Heap Java Example
Let us construct a Min Heap using numbers 21, 11, 5 19, 18, 14, 9.
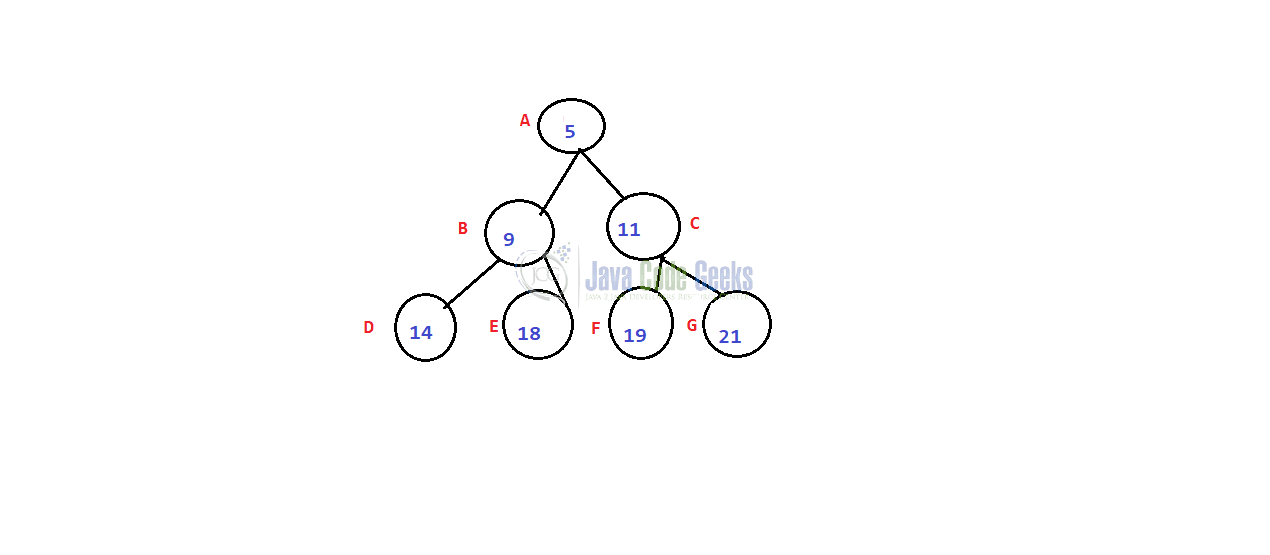
In this example, the value at node A is 5 and it has children B and C with 9 and 11 respectively. According to Min Heap property, the parent node has a value lesser than that of values at children which are 9 and 11. Coming to node B which has a value 9, it is lesser than that of values at its children D and E with 14 and 18 respectively. Coming to node C which has a value 11, it is lesser than that of its children F and G with values 19 and 21. so every node satisfies the Min Heap condition.
3. Methods or Operations on Heap
- find – find an item in a heap.
- insert – add an item in a heap ensuring the heap property is maintained min-heap and max-heap property.
- delete – remove an item in a heap.
- extract – return the value of an item and then delete it from the heap.
- replace – extract or pop the root and insert or push a new item in a heap ensuring the heap property has maintained min-heap and max-heap property.
Apart from the above mentioned basic operations, there are other operations such as:
- size – returns the size of a heap.
- is-empty – returns ‘true’ if heap is empty or ‘false’ if it has value.
- merge – joining or union of two heaps, all the values from both heaps are included but the original heaps are preserved.
- meld – joining of two heaps where the values from both heaps are included but the original heaps are destroyed.
4. Representation and Implementation
A Min Heap is typically represented as an array. The root element will be at Arr[0]. For any ith node, i.e., Arr[i]:
- Arr[(i -1) / 2] returns its parent node.
- Arr[(2 * i) + 1] returns its left child node.
- Arr[(2 * i) + 2] returns its right child node.
In Java, we can implement Min Heap with and without using Library Functions.
4.1 Without Library Function
Consider the following code which implements Min Heap in Java without using any predefined Library functions of Java.
MinHeap1.java
// Java implementation of Min Heap
class MinHeap {
private int[] Heap;
private int size;
private int maxsize;
private static final int FRONT = 1;
public MinHeap(int maxsize)
{
this.maxsize = maxsize;
this.size = 0;
Heap = new int[this.maxsize + 1];
Heap[0] = Integer.MIN_VALUE;
}
// Function to return the position of
// the parent for the node currently
// at pos
private int parent(int pos)
{
return pos / 2;
}
// Function to return the position of the
// left child for the node currently at pos
private int leftChild(int pos)
{
return (2 * pos);
}
// Function to return the position of
// the right child for the node currently
// at pos
private int rightChild(int pos)
{
return (2 * pos) + 1;
}
// Function that returns true if the passed
// node is a leaf node
private boolean isLeaf(int pos)
{
if (pos >= (size / 2) && pos <= size) {
return true;
}
return false;
}
// Function to swap two nodes of the heap
private void swap(int fpos, int spos)
{
int tmp;
tmp = Heap[fpos];
Heap[fpos] = Heap[spos];
Heap[spos] = tmp;
}
// Function to heapify the node at pos
private void minHeapify(int pos)
{
// If the node is a non-leaf node and greater
// than any of its child
if (!isLeaf(pos)) {
if (Heap[pos] > Heap[leftChild(pos)]
|| Heap[pos] > Heap[rightChild(pos)]) {
// Swap with the left child and heapify
// the left child
if (Heap[leftChild(pos)] < Heap[rightChild(pos)]) {
swap(pos, leftChild(pos));
minHeapify(leftChild(pos));
}
// Swap with the right child and heapify
// the right child
else {
swap(pos, rightChild(pos));
minHeapify(rightChild(pos));
}
}
}
}
// Function to insert a node into the heap
public void insert(int element)
{
if (size >= maxsize) {
return;
}
Heap[++size] = element;
int current = size;
while (Heap[current] < Heap[parent(current)]) {
swap(current, parent(current));
current = parent(current);
}
}
// Function to print the contents of the heap
public void print()
{
for (int i = 1; i <= size / 2; i++) {
System.out.print(" PARENT : " + Heap[i]
+ " LEFT CHILD : " + Heap[2 * i]
+ " RIGHT CHILD :" + Heap[2 * i + 1]);
System.out.println();
}
}
// Function to build the min heap using
// the minHeapify
public void minHeap()
{
for (int pos = (size / 2); pos >= 1; pos--) {
minHeapify(pos);
}
}
// Function to remove and return the minimum
// element from the heap
public int remove()
{
int popped = Heap[FRONT];
Heap[FRONT] = Heap[size--];
minHeapify(FRONT);
return popped;
}
// Driver code
public static void main(String[] arg)
{
System.out.println("The Min Heap is ");
MinHeap minHeap = new MinHeap(15);
minHeap.insert(5);
minHeap.insert(3);
minHeap.insert(17);
minHeap.insert(10);
minHeap.insert(84);
minHeap.insert(19);
minHeap.insert(6);
minHeap.insert(22);
minHeap.insert(9);
minHeap.minHeap();
minHeap.print();
System.out.println("The Min val is " + minHeap.remove());
}
}
Output
The Min Heap is PARENT : 3 LEFT CHILD : 5 RIGHT CHILD :6 PARENT : 5 LEFT CHILD : 9 RIGHT CHILD :84 PARENT : 6 LEFT CHILD : 19 RIGHT CHILD :17 PARENT : 9 LEFT CHILD : 22 RIGHT CHILD :10 The Min val is 3
2.2 Using Library Functions
We can implement Min Heap using PriorityQueue class from java.util package. By default Min Heap is implemented by this class.
MinHeap2.java
// Java program to demonstrate working of PriorityQueue
import java.util.*;
class MinHeap2 {
// Driver code
public static void main(String args[])
{
// Creating empty priority queue
PriorityQueue pQueue = new PriorityQueue();
// Adding items to the pQueue using add()
pQueue.add(10);
pQueue.add(30);
pQueue.add(20);
pQueue.add(400);
// Printing the most priority element
System.out.println("Head value using peek function:" + pQueue.peek());
// Printing all elements
System.out.println("The queue elements:");
Iterator itr = pQueue.iterator();
while (itr.hasNext())
System.out.println(itr.next());
// Removing the top priority element (or head) and
// printing the modified pQueue using poll()
pQueue.poll();
System.out.println("After removing an element "
+ "with poll function:");
Iterator itr2 = pQueue.iterator();
while (itr2.hasNext())
System.out.println(itr2.next());
// Removing 30 using remove()
pQueue.remove(30);
System.out.println("after removing 30 with"
+ " remove function:");
Iterator itr3 = pQueue.iterator();
while (itr3.hasNext())
System.out.println(itr3.next());
// Check if an element is present using contains()
boolean b = pQueue.contains(20);
System.out.println("Priority queue contains 20 "
+ "or not?: " + b);
// Getting objects from the queue using toArray()
// in an array and print the array
Object[] arr = pQueue.toArray();
System.out.println("Value in array: ");
for (int i = 0; i < arr.length; i++)
System.out.println("Value: " + arr[i].toString());
}
} Output
Head value using peek function:10 The queue elements: 10 30 20 400 After removing an element with poll function: 20 30 400 after removing 30 with remove function: 20 400 Priority queue contains 20 or not?: true Value in array: Value: 20 Value: 400
5. Applications
- Heap is used in sorting algorithms like Heapsort.
- A Heap allows access to the min or max element in constant time, and other selections (such as median or kth-element) can be done using a Heap.
- Graph Algorithms like Prim’s-minimal-spanning-tree algorithm and Dijkstra’s shortest-path algorithm can be implemented using a Heap.
- PriorityQueues can be implemented using a Heap.
- Heap can be used to find the smallest or the largest element in an array.
6. Summary
In this article, we understood Heap data structure, its types, and its representation with an example. Then we have seen operations or methods and implemented Min Heap in java with and without library function. Finally, we understood about applications of a Heap.
7. More articles
- Java Tutorial for Beginners (with video)
- Best Way to Learn Java Programming Online
- Java Array – java.util.Arrays Example (with Video)
- Java List Example
- Java Map Example
- Java Queue Example (with video)
- Java Stack Example (with video)
8. Download the Source Code
This is an example of Min Heap in java.
You can download the full source code of this example here: Min Heap Java Example
Last updated on Jul. 26th, 2021



good article