Selection Sort Java Example
1. Introduction
Selection sort Java ‘s simple algorithm can divide the array into sorted and unsorted parts. Initially, the sorted part is empty; the unsorted part is the entire array. It starts by finding the smallest element from the unsorted part and swaps it with the left-most element of the unsorted part. Each finding reduces the unsorted part by one. It ends when the unsorted part is empty.
Time and space complexities are used when analyzing algorithms. A time complexity measures the amount of time it takes to run an algorithm in relation to the input size. A space complexity measures the magnitude of auxiliary space the program takes to process the inputs.
Here are the steps to sort an array with three elements: {34, 56, 12}.
- The unsorted part is the entire array.
- Find the smallest element from the unsorted part. In this step, it’s 12.
- Swap the left-most of the unsorted array with the smallest number. In this step, it swaps 34 and 12, so the array becomes {12, 56, 34}. The sorted part is {12} and the unsorted part is {56, 34}.
- Find the smallest element from the unsorted part. In this step, it’s 34.
- Swap the left-most of the unsorted array with the smallest number. In this step, it swaps 56 and 34.
- The array is sorted. It is {12, 34, 56}.
As you have seen in the example, there are (N – 1) comparing operations and one additional variable when finding the smallest number from N elements. It will iterate (N – 1) times; each iteration has one smaller number to check and three swapping operations. So the total number of comparing operations is N + (N-1) + (N-2) + … + 1, which equals to N * ( N-1) / 2. The total number of swapping operation is 3 * N. Big O annotation cares about the dominant term. Therefore, the time complexity of the algorithm selection sort is O(n^2). The space complexity is O(1) because it only needs two additional variables.
In this example, I will create a Maven project to demonstrate how to sort an integer array with the algorithm: Selection Sort, Bubble Sort, Insertion Sort, and Quick Sort. I will also demonstrate how to sort a Card array with the Selection Sort algorithm.
2. Technologies Used
The example code in this article was built and run using:
- Java 11
- Maven 3.3.9
- Junit 4.12
- Jfreechart 1.5.0
- Eclipse Oxygen
3. Maven Project
In this step, I will create a Maven project which includes several classes to demonstrate the Selection Sort algorithm. I will use Jfreechart to show the results in a line graph.
3.1 Dependencies
I will include Junit and Jfreechart in the pom.xml.
pom.xml
<project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd"> <modelVersion>4.0.0</modelVersion> <groupId>org.jcg.zheng.demo</groupId> <artifactId>selection-sort</artifactId> <version>0.0.1-SNAPSHOT</version> <properties> <project.build.sourceEncoding>UTF-8</project.build.sourceEncoding> </properties> <build> <sourceDirectory>src</sourceDirectory> <plugins> <plugin> <artifactId>maven-compiler-plugin</artifactId> <version>3.8.0</version> <configuration> <release>11</release> </configuration> </plugin> </plugins> </build> <dependencies> <dependency> <groupId>junit</groupId> <artifactId>junit</artifactId> <version>4.12</version> </dependency> <dependency> <groupId>org.jfree</groupId> <artifactId>jfreechart</artifactId> <version>1.5.0</version> </dependency> </dependencies> </project>
3.2 Utils
In this step, I will create an Utils class to define four text files which store the execution time for each sorting test. The data will be used to draw a line graph later. It also has an isSortedAsc method to check if an array is sorted by the ascending order.
Utils.java
package org.jcg.zheng;
import java.util.stream.IntStream;
public class Utils {
public static final String BULLBLE_SORT_TIME = "BubbleSort.csv";
public static final String INSERTION_SORT_TIME = "InsertionSort.csv";
public static final String QUICK_SORT_TIME = "QuickSort.csv";
public static final String SELECTION_SORT_TIME = "SelectionSort.csv";
public static boolean isSortedAsc(int[] intArray) {
return IntStream.range(0, intArray.length - 1).noneMatch(i -> intArray[i] > intArray[i + 1]);
}
}
3.3 LineGraphChart
In this step, I will create a LineGraphChart class which extends from org.jfree.chart.ui.ApplicationFrame. It will draw line graphs for given xy coordinates from the test classes. The xy coordinates are the input size N vs the execution time captured during testing.
LineGraphChart.java
package org.jcg.zheng;
import java.awt.BorderLayout;
import java.awt.Color;
import java.io.File;
import java.io.IOException;
import java.nio.charset.Charset;
import java.nio.file.Files;
import java.util.HashMap;
import java.util.Map;
import javax.swing.JPanel;
import org.jfree.chart.ChartFactory;
import org.jfree.chart.ChartPanel;
import org.jfree.chart.JFreeChart;
import org.jfree.chart.axis.NumberAxis;
import org.jfree.chart.axis.ValueAxis;
import org.jfree.chart.plot.PlotOrientation;
import org.jfree.chart.plot.XYPlot;
import org.jfree.chart.renderer.xy.StandardXYItemRenderer;
import org.jfree.chart.ui.ApplicationFrame;
import org.jfree.data.xy.XYDataset;
import org.jfree.data.xy.XYSeries;
import org.jfree.data.xy.XYSeriesCollection;
public class LineGraphChart extends ApplicationFrame {
private static final long serialVersionUID = 8024827403766653799L;
public static void main(String[] args) {
final LineGraphChart demo = new LineGraphChart("Sorting - Big O");
demo.pack();
demo.setVisible(true);
}
private XYPlot plot;
public LineGraphChart(String title) {
super(title);
final XYDataset dataset1 = createRandomDataset("SelectionSort", readCoordinates(Utils.SELECTION_SORT_TIME));
final JFreeChart chart = ChartFactory.createXYLineChart("Big O Notations", "Input Size", "Value", dataset1,
PlotOrientation.VERTICAL, true, true, false);
chart.setBackgroundPaint(Color.white);
this.plot = chart.getXYPlot();
this.plot.setBackgroundPaint(Color.lightGray);
this.plot.setDomainGridlinePaint(Color.white);
this.plot.setRangeGridlinePaint(Color.white);
final ValueAxis axis = this.plot.getDomainAxis();
axis.setAutoRange(true);
final NumberAxis rangeAxis2 = new NumberAxis("Range Axis 2");
rangeAxis2.setAutoRangeIncludesZero(false);
final JPanel content = new JPanel(new BorderLayout());
final ChartPanel chartPanel = new ChartPanel(chart);
content.add(chartPanel);
chartPanel.setPreferredSize(new java.awt.Dimension(700, 500));
setContentPane(content);
this.plot.setDataset(1, createRandomDataset("BubbleSort", readCoordinates(Utils.BULLBLE_SORT_TIME)));
this.plot.setRenderer(1, new StandardXYItemRenderer());
this.plot.setDataset(2, createRandomDataset("InsertionSort", readCoordinates(Utils.INSERTION_SORT_TIME)));
this.plot.setRenderer(2, new StandardXYItemRenderer());
this.plot.setDataset(3, createRandomDataset("QuickSort", readCoordinates(Utils.QUICK_SORT_TIME)));
this.plot.setRenderer(3, new StandardXYItemRenderer());
}
private XYDataset createRandomDataset(final String label, Map<Long, Long> xyCoordinates) {
XYSeriesCollection dataset = new XYSeriesCollection();
XYSeries series = new XYSeries(label);
xyCoordinates.forEach((k, v) -> {
series.add(k, v);
});
dataset.addSeries(series);
return dataset;
}
private Map<Long, Long> readCoordinates(String filename) {
Map<Long, Long> xyCoordinates = new HashMap<>();
try {
File data = new File(filename);
Files.readAllLines(data.toPath(), Charset.defaultCharset()).forEach(s -> {
String[] values = s.split(",");
xyCoordinates.put(Long.valueOf(values[0]), Long.valueOf(values[1]));
});
} catch (IOException e) {
e.printStackTrace();
}
return xyCoordinates;
}
}
3.4 Card
In this step, I will create a Card class which has two data members: color and number.
Card.java
package org.jcg.zheng;
public class Card {
private String color;
private int number;
public Card(String color, int number) {
super();
this.color = color;
this.number = number;
}
public String getColor() {
return color;
}
public int getNumber() {
return number;
}
public void setColor(String color) {
this.color = color;
}
public void setNumber(int number) {
this.number = number;
}
@Override
public String toString() {
return "Card [color=" + color + ", number=" + number + "]";
}
}
4. Sorting Algorithms
4.1 Selection Sort algorithm in Java
In this step, I will create a SelectionSort class which has two methods:
findMinimumFromUnSortedPart(int[] intArray, int startIndexOfUnSorted)– It finds the smallest element in a given array from the starting index of the unsorted part. The max operation is N – 1. This step scans all elements. If the elements change, then have to redo. In this case, Insertion sort is a better choice.sortAsc(int[] intArray)– It iterates the array and swaps the left-most element in the unsorted part to the smallest element found for each iteration.
SelectionSort.java
package org.jcg.zheng.sort;
/**
* Selection Sort divides the array into a sorted and unsorted sub-array. The
* sorted sub-array is formed by inserting the minimum element of the unsorted
* sub-array at the end of the sorted array
*
*/
public class SelectionSort {
private int findMinimumFromUnSortedPart(int[] numberArray, int startIndexOfUnSorted) {
// Find the minimum element's index in unsorted array
int minIndex = startIndexOfUnSorted;
// each find will scan the unsorted array only
for (int j = startIndexOfUnSorted + 1; j < numberArray.length; j++) {
if (numberArray[j] < numberArray[minIndex]) {
minIndex = j;
}
}
return minIndex;
}
public void sortAsc(int numberArray[]) {
// One by one move boundary of unsorted sub-array
for (int i = 0; i < numberArray.length - 1; i++) {
int minIndex = findMinimumFromUnSortedPart(numberArray, i);
// Swap the found minimum element with the element,
// so the front part of array is sorted
int temp = numberArray[minIndex];
numberArray[minIndex] = numberArray[i];
numberArray[i] = temp;
}
}
}
4.2 Insertion Sort algorithm in Java
In this step, I will create an InsertionSort class which has two methods:
isOutOfOrder(int sortedValue, int checkValue)– It compares thesortedValuetocheckValue. It returns true if thesortedValueis greater than thecheckValue.sortAsc(int[] intArray)– It assumes the array is sorted in the beginning. It iterates the array and checks if the element is in-order or not, if it is out of order, then places the element in the correct location for the sorted part. There are two loops. The outer loop repeats (N -1) times. The inner loop repeats to find the correct location in the sorted part. The time complexity is O(n^2).
Here are the steps to sort an integer array: {34, 56, 12}.
- The sorted part has the first element at the beginning. In this step, it’s 34.
- It checks the second element. In this case, 56 is ordered, then the sorted part is {34, 56}.
- It checks the last element. In this case, 12 is not ordered. It compares the elements in the sorted array and moves other elements and places it at the correct location. The sorted part is {12, 34, 56}.
- It ends as the array is sorted now.
As you can see here, if the original array changes by adding new elements, the insertion sort will be faster as it reduces the comparison operations.
InsertionSort.java
package org.jcg.zheng.sort;
/**
* The idea behind Insertion Sort is dividing the array into the sorted and
* unsorted sub-arrays.
*
* The sorted part is of length 1 at the beginning and is corresponding to the
* first (left-most) element in the array. We iterate through the array and
* during each iteration, we expand the sorted portion of the array by one
* element.
*
* Upon expanding, we place the new element into its proper place within the
* sorted sub-array. We do this by shifting all of the elements to the right
* until we encounter the first element we don't have to shift.
*
*
*/
public class InsertionSort {
boolean isOutOfOrder(int sortedValue, int checkValue) {
return sortedValue > checkValue;
}
public void sortAsc(int numberArray[]) {
for (int i = 1; i < numberArray.length; ++i) {
// the elements from index 0 to sortedIndex are sorted ascending
int whereShouldIBe = i - 1;
int checkValue = numberArray[i];
while (whereShouldIBe >= 0 && isOutOfOrder(numberArray[whereShouldIBe], checkValue)) {
numberArray[whereShouldIBe + 1] = numberArray[whereShouldIBe];
whereShouldIBe = whereShouldIBe - 1;
}
// reposition the checkValue in the sorted part
numberArray[whereShouldIBe + 1] = checkValue;
}
}
}
4.3 Bubble Sort algorithm in Java
In this step, I will create a BubbleSort class which has two methods:
isOutOfOrder(int frontNumber, int backNumber)– It compares thefrontNumbertobackNumber.sortAsc(int[] intArray)– It iterates the array and swaps the adjacent elements if they are out of order. It has two loops, so the time complexity is O (n^2).
Here are the steps to sort an integer array: {34, 56, 12}.
- It compares the first two elements: 34 and 56. It’s ordered.
- It compares the 56 and 12, It’s out-of-order, so it swaps 56 and 12 and became {34, 12, 56}.
- It compares the 34 and 12, it’s out-of-order, so it swaps 34 and 12 and became {12, 34, 56}.
As you can see here, if the original array is sorted, then Bubble sort will reduce the comparison step at the inner loop.
BubbleSort.java
package org.jcg.zheng.sort;
/**
* Bubble sort works by swapping adjacent elements if they're not in the desired
* order. This process repeats from the beginning of the array until all
* elements are in order.
*
* We know that all elements are in order when we manage to do the whole
* iteration without swapping at all - then all elements we compared were in the
* desired order with their adjacent elements, and by extension, the whole
* array.
*
*
*/
public class BubbleSort {
private boolean isOutOfOrder(int frontNumber, int backNumber) {
return frontNumber > backNumber;
}
public void sortAsc(int[] numberArray) {
int temp = 0;
for (int i = 0; i < numberArray.length; i++) {
for (int j = 1; j < (numberArray.length - i); j++) {
if (isOutOfOrder(numberArray[j - 1], numberArray[j])) {
temp = numberArray[j - 1];
numberArray[j - 1] = numberArray[j];
numberArray[j] = temp;
}
}
}
}
}4.4 Quick Sort algorithm in Java
In this step, I will create a QuickSort class which has three methods:
swapNumbers(int i, int j)– it swaps the elements position in a given array.quickSort(int low, int high)– It divides into two sub-array from the mid-point, then swaps the low and high position if they are out of order. It recursively sort the sub-list. The time complexity is O(log n).sortAsc(int[] intArray)– It starts with 0 sorted part and calls thequickSortmethod recursively to sort the array.
Here are the steps to sort {34, 56, 12}.
- Find the middle element. In this step 56.
- Compare the low part to the middle. In this step, 34 is smaller than 56, then increase the low index by 1.
- Compare the high to the middle. In this step, 12 is smaller than 56, then need to swap, it became {34, 12, 56}.
- Repeat the steps for {34, 12}, It swaps again to {12, 34, 56}
- Stop as the low index is greater than the high index.
QuickSort.java
package org.jcg.zheng.sort;
/**
* QuickSort or partition-exchange sort, is a fast sorting algorithm, which is
* using divide and conquer algorithm. QuickSort first divides a large list into
* two smaller sub-lists: the low elements and the high elements. QuickSort can
* then recursively sort the sub-lists.
*
*/
public class QuickSort {
private int array[];
private int length;
private void quickSort(int lowerIndex, int higherIndex) {
int low = lowerIndex;
int high = higherIndex;
int midPoint_As_Pivot = array[lowerIndex + (higherIndex - lowerIndex) / 2];
while (low <= high) {
/**
* In each iteration, we will identify a number from left side which is greater
* then the pivot value, and also we will identify a number from right side
* which is less then the pivot value. Once the search is done, then we exchange
* both numbers.
*/
while (array[low] < midPoint_As_Pivot) {
low++;
}
while (array[high] > midPoint_As_Pivot) {
high--;
}
if (low <= high) {
swapNumbers(low, high);
// move index to next position on both sides
low++;
high--;
}
}
// call quickSort() method recursively
if (lowerIndex < high) {
quickSort(lowerIndex, high);
}
if (low < higherIndex) {
quickSort(low, higherIndex);
}
}
public void sortAsc(int[] inputArr) {
if (inputArr == null || inputArr.length == 0) {
return;
}
this.array = inputArr;
this.length = inputArr.length;
quickSort(0, length - 1);
}
private void swapNumbers(int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}4.5 Selection Sort on Cards
In this step, I will create SelectionSortPojo class to sort a Card array. It has a similar logic as SelectionSort. I will use it to demonstrate the non-stability of algorithm.
SelectionSortPojo.java
package org.jcg.zheng.sort;
import org.jcg.zheng.Card;
public class SelectionSortPojo {
private int findMinimumFromStartIndex(Card[] cards, int startIndex) {
// Find the minimum element's index in unsorted array
int min_idx = startIndex;
// each find will scan the unsorted array only
for (int j = startIndex + 1; j < cards.length; j++) {
if (cards[j].getNumber() < cards[min_idx].getNumber()) {
min_idx = j;
}
}
return min_idx;
}
public void sortAsc(Card[] cards) {
// One by one move boundary of unsorted sub-array
for (int i = 0; i < cards.length - 1; i++) {
int min_idx = findMinimumFromStartIndex(cards, i);
// Swap the found minimum element with the element,
// so the first part of array is sorted
Card temp = cards[min_idx];
cards[min_idx] = cards[i];
cards[i] = temp;
}
}
}5. JUnit Test
In this step, I will use parameterized Junit tests to capture the methods execution time when the input size grows. I will use Jfreechart to draw a time complexity graph for SelectionSort, InsertationSort, BubbleSort, and QuickSort.
5.1 TestBase
In this step, I will create a TestBase class which starts the execute time clock before and after each test. It saves the input size and execution time in a file to draw them in a graph. It also defines input size array to be used in a parameter tests for these 4 algorithms.
setup()– captures the start timecleanup()– captures the finish time and save the input size to the execution time in a filesetArray()– constructs an integer arraywriteFile()– writes the execution time for each testTEST_SIZE_PARAMETER– is a variable used by theParameterizedtest, so the test can be executed multiple times, one for each parameter. Here I define the input sizes from 10, 200, 300, 500, 800, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000, 11000, 12000, 13000, 14000, 15000, 16000, 17000, 18000, 19000, to 200000.
TestBase.java
package org.jcg.zheng.sort;
import static org.junit.Assert.assertFalse;
import static org.junit.Assert.assertTrue;
import java.io.FileWriter;
import java.io.IOException;
import java.time.Duration;
import java.time.Instant;
import java.util.Arrays;
import java.util.List;
import java.util.Random;
import org.jcg.zheng.Utils;
import org.junit.After;
import org.junit.Before;
import org.junit.Rule;
import org.junit.rules.TestName;
public abstract class TestBase {
protected static final List<Object[]> TEST_SIZE_PARAMETER = Arrays
.asList(new Object[][] { { 10 }, { 200 }, { 300 }, { 500 }, { 800 }, { 1000 }, { 2000 }, { 3000 }, { 4000 },
{ 5000 }, { 6000 }, { 7000 }, { 8000 }, { 9000 }, { 10000 }, { 11000 }, { 12000 }, { 13000 },
{ 14000 }, { 15000 }, { 16000 }, { 17000 }, { 18000 }, { 19000 }, { 20000 }, { 30000 }, { 40000 },
{ 50000 }, { 60000 }, { 70000 }, { 80000 }, { 90000 }, { 100000 }, { 110000 }, { 120000 },
{ 130000 }, { 140000 }, { 150000 }, { 160000 }, { 170000 }, { 180000 } });
protected String filename;
private Instant finishTime;
protected int[] integerArray;
@Rule
public TestName name = new TestName();
protected int nSize;
protected Random randam = new Random();
private Instant startTime;
@After
public void cleanup() {
finishTime = Instant.now();
assertTrue(Utils.isSortedAsc(integerArray));
long totalTimeInNs = Duration.between(startTime, finishTime).toNanos();
System.out.printf("\t%s with nSize =%d completed in %d ns\n", name.getMethodName(), nSize, totalTimeInNs);
if (totalTimeInNs > 0) {
String line = nSize + "," + totalTimeInNs + "\n";
writeFile(filename, line);
}
}
private int[] setArray(int arraySize) {
int nSize = arraySize;
int[] items = new int[nSize];
for (int i = 0; i < nSize; i++) {
items[i] = randam.nextInt(10000);
}
return items;
}
@Before
public void setup() {
integerArray = setArray(this.nSize);
assertFalse(Utils.isSortedAsc(integerArray));
startTime = Instant.now();
}
protected void writeFile(String filename, String content) {
try {
FileWriter fw = new FileWriter(filename, true);
fw.write(content);
fw.close();
} catch (IOException ioe) {
System.err.println("IOException: " + ioe.getMessage());
}
}
}
5.2 Selection Sort Test
In this step, I will create a SelectionSortTest to test sortAsc. It extends from TestBase and executes the test repeatedly for various inputs.
SelectionSortTest.java
package org.jcg.zheng.sort;
import java.util.Collection;
import org.jcg.zheng.Utils;
import org.junit.Before;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runners.Parameterized;
@RunWith(Parameterized.class)
public class SelectionSortTest extends TestBase {
@Parameterized.Parameters
public static Collection input() {
return TEST_SIZE_PARAMETER;
}
private SelectionSort testClass;
public SelectionSortTest(int nSize) {
super();
this.nSize = nSize;
}
@Test
public void selectionSort_Asc() {
testClass.sortAsc(integerArray);
}
@Before
public void setup() {
testClass = new SelectionSort();
this.filename = Utils.SELECTION_SORT_TIME;
super.setup();
}
}Output
selectionSort_Asc[0] with nSize =10 completed in 0 ns selectionSort_Asc[1] with nSize =200 completed in 0 ns selectionSort_Asc[2] with nSize =300 completed in 0 ns selectionSort_Asc[3] with nSize =500 completed in 1998000 ns selectionSort_Asc[4] with nSize =800 completed in 4998000 ns selectionSort_Asc[5] with nSize =1000 completed in 998900 ns selectionSort_Asc[6] with nSize =2000 completed in 1996600 ns selectionSort_Asc[7] with nSize =3000 completed in 6996900 ns selectionSort_Asc[8] with nSize =4000 completed in 13995200 ns selectionSort_Asc[9] with nSize =5000 completed in 13997100 ns selectionSort_Asc[10] with nSize =6000 completed in 22001400 ns selectionSort_Asc[11] with nSize =7000 completed in 23995600 ns selectionSort_Asc[12] with nSize =8000 completed in 40000700 ns selectionSort_Asc[13] with nSize =9000 completed in 43995100 ns selectionSort_Asc[14] with nSize =10000 completed in 56995100 ns selectionSort_Asc[15] with nSize =11000 completed in 85999500 ns selectionSort_Asc[16] with nSize =12000 completed in 83996100 ns selectionSort_Asc[17] with nSize =13000 completed in 90995800 ns selectionSort_Asc[18] with nSize =14000 completed in 86998700 ns selectionSort_Asc[19] with nSize =15000 completed in 105022100 ns selectionSort_Asc[20] with nSize =16000 completed in 166997700 ns selectionSort_Asc[21] with nSize =17000 completed in 129974600 ns selectionSort_Asc[22] with nSize =18000 completed in 146997900 ns selectionSort_Asc[23] with nSize =19000 completed in 148002000 ns selectionSort_Asc[24] with nSize =20000 completed in 176997200 ns selectionSort_Asc[25] with nSize =30000 completed in 419993900 ns selectionSort_Asc[26] with nSize =40000 completed in 647998100 ns selectionSort_Asc[27] with nSize =50000 completed in 983023100 ns selectionSort_Asc[28] with nSize =60000 completed in 1490973400 ns selectionSort_Asc[29] with nSize =70000 completed in 1999993400 ns selectionSort_Asc[30] with nSize =80000 completed in 2530997800 ns selectionSort_Asc[31] with nSize =90000 completed in 3137977600 ns selectionSort_Asc[32] with nSize =100000 completed in 3876998900 ns selectionSort_Asc[33] with nSize =110000 completed in 4913997200 ns selectionSort_Asc[34] with nSize =120000 completed in 5721998200 ns selectionSort_Asc[35] with nSize =130000 completed in 7307997000 ns selectionSort_Asc[36] with nSize =140000 completed in 8279000300 ns selectionSort_Asc[37] with nSize =150000 completed in 8951992600 ns selectionSort_Asc[38] with nSize =160000 completed in 10402002100 ns selectionSort_Asc[39] with nSize =170000 completed in 11452002600 ns selectionSort_Asc[40] with nSize =180000 completed in 13425003000 ns
5.3 Insertion Sort Test
In this step, I will create an InsertSortTest to test sortAsc. It extends from TestBase and executes the test repeatedly for various inputs.
InsertionSortTest.java
package org.jcg.zheng.sort;
import java.util.Collection;
import org.jcg.zheng.Utils;
import org.junit.Before;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runners.Parameterized;
@RunWith(Parameterized.class)
public class InsertionSortTest extends TestBase {
@Parameterized.Parameters
public static Collection input() {
return TEST_SIZE_PARAMETER;
}
private InsertionSort testClass;
public InsertionSortTest(int nSize) {
super();
this.nSize = nSize;
}
@Test
public void insertionSort_Asc() {
testClass.sortAsc(integerArray);
}
@Before
public void setup() {
testClass = new InsertionSort();
this.filename = Utils.INSERTION_SORT_TIME;
super.setup();
}
}Output
insertionSort_Asc[0] with nSize =10 completed in 0 ns insertionSort_Asc[1] with nSize =200 completed in 999800 ns insertionSort_Asc[2] with nSize =300 completed in 2001900 ns insertionSort_Asc[3] with nSize =500 completed in 8997200 ns insertionSort_Asc[4] with nSize =800 completed in 3001600 ns insertionSort_Asc[5] with nSize =1000 completed in 4998000 ns insertionSort_Asc[6] with nSize =2000 completed in 7997400 ns insertionSort_Asc[7] with nSize =3000 completed in 2997000 ns insertionSort_Asc[8] with nSize =4000 completed in 3996300 ns insertionSort_Asc[9] with nSize =5000 completed in 5997300 ns insertionSort_Asc[10] with nSize =6000 completed in 11998700 ns insertionSort_Asc[11] with nSize =7000 completed in 9997700 ns insertionSort_Asc[12] with nSize =8000 completed in 12999400 ns insertionSort_Asc[13] with nSize =9000 completed in 19998300 ns insertionSort_Asc[14] with nSize =10000 completed in 20995000 ns insertionSort_Asc[15] with nSize =11000 completed in 24998500 ns insertionSort_Asc[16] with nSize =12000 completed in 33996600 ns insertionSort_Asc[17] with nSize =13000 completed in 43000700 ns insertionSort_Asc[18] with nSize =14000 completed in 54998900 ns insertionSort_Asc[19] with nSize =15000 completed in 40997800 ns insertionSort_Asc[20] with nSize =16000 completed in 49999500 ns insertionSort_Asc[21] with nSize =17000 completed in 52998600 ns insertionSort_Asc[22] with nSize =18000 completed in 59993600 ns insertionSort_Asc[23] with nSize =19000 completed in 58996000 ns insertionSort_Asc[24] with nSize =20000 completed in 65999200 ns insertionSort_Asc[25] with nSize =30000 completed in 142993600 ns insertionSort_Asc[26] with nSize =40000 completed in 292997500 ns insertionSort_Asc[27] with nSize =50000 completed in 503999900 ns insertionSort_Asc[28] with nSize =60000 completed in 808000300 ns insertionSort_Asc[29] with nSize =70000 completed in 907021800 ns insertionSort_Asc[30] with nSize =80000 completed in 1110971600 ns insertionSort_Asc[31] with nSize =90000 completed in 1834000300 ns insertionSort_Asc[32] with nSize =100000 completed in 1804999900 ns insertionSort_Asc[33] with nSize =110000 completed in 1917005700 ns insertionSort_Asc[34] with nSize =120000 completed in 2159026400 ns insertionSort_Asc[35] with nSize =130000 completed in 2805973000 ns insertionSort_Asc[36] with nSize =140000 completed in 3186001400 ns insertionSort_Asc[37] with nSize =150000 completed in 3502998300 ns insertionSort_Asc[38] with nSize =160000 completed in 3897997900 ns insertionSort_Asc[39] with nSize =170000 completed in 4279001700 ns insertionSort_Asc[40] with nSize =180000 completed in 4845996100 ns
5.4 Bubble Sort Test
In this step, I will create a BubbleSortTest to test sortAsc. It extends from TestBase and executes the test repeatedly for various inputs.
BubbleSortTest.java
package org.jcg.zheng.sort;
import java.util.Collection;
import org.jcg.zheng.Utils;
import org.junit.Before;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runners.Parameterized;
@RunWith(Parameterized.class)
public class BubbleSortTest extends TestBase {
@Parameterized.Parameters
public static Collection input() {
return TEST_SIZE_PARAMETER;
}
private BubbleSort testClass;
public BubbleSortTest(int nSize) {
super();
this.nSize = nSize;
}
@Test
public void bubbleSort_Asc() {
testClass.sortAsc(integerArray);
}
@Before
public void setup() {
testClass = new BubbleSort();
this.filename = Utils.BULLBLE_SORT_TIME;
super.setup();
}
}
Output
bubbleSort_Asc[0] with nSize =10 completed in 0 ns bubbleSort_Asc[1] with nSize =200 completed in 2001100 ns bubbleSort_Asc[2] with nSize =300 completed in 4999600 ns bubbleSort_Asc[3] with nSize =500 completed in 1993800 ns bubbleSort_Asc[4] with nSize =800 completed in 2998800 ns bubbleSort_Asc[5] with nSize =1000 completed in 13000600 ns bubbleSort_Asc[6] with nSize =2000 completed in 6995900 ns bubbleSort_Asc[7] with nSize =3000 completed in 14999000 ns bubbleSort_Asc[8] with nSize =4000 completed in 27995400 ns bubbleSort_Asc[9] with nSize =5000 completed in 50000200 ns bubbleSort_Asc[10] with nSize =6000 completed in 86999300 ns bubbleSort_Asc[11] with nSize =7000 completed in 182998900 ns bubbleSort_Asc[12] with nSize =8000 completed in 246997300 ns bubbleSort_Asc[13] with nSize =9000 completed in 180003400 ns bubbleSort_Asc[14] with nSize =10000 completed in 194993200 ns bubbleSort_Asc[15] with nSize =11000 completed in 259998700 ns bubbleSort_Asc[16] with nSize =12000 completed in 301999200 ns bubbleSort_Asc[17] with nSize =13000 completed in 626000400 ns bubbleSort_Asc[18] with nSize =14000 completed in 462994700 ns bubbleSort_Asc[19] with nSize =15000 completed in 454997700 ns bubbleSort_Asc[20] with nSize =16000 completed in 580991000 ns bubbleSort_Asc[21] with nSize =17000 completed in 564986600 ns bubbleSort_Asc[22] with nSize =18000 completed in 678990900 ns bubbleSort_Asc[23] with nSize =19000 completed in 754000100 ns bubbleSort_Asc[24] with nSize =20000 completed in 866001800 ns bubbleSort_Asc[25] with nSize =30000 completed in 1982988800 ns bubbleSort_Asc[26] with nSize =40000 completed in 3852991500 ns bubbleSort_Asc[27] with nSize =50000 completed in 5633003400 ns bubbleSort_Asc[28] with nSize =60000 completed in 8055000600 ns bubbleSort_Asc[29] with nSize =70000 completed in 10573973400 ns bubbleSort_Asc[30] with nSize =80000 completed in 14025005000 ns bubbleSort_Asc[31] with nSize =90000 completed in 15945001700 ns bubbleSort_Asc[32] with nSize =100000 completed in 20088999700 ns bubbleSort_Asc[33] with nSize =110000 completed in 24282000900 ns bubbleSort_Asc[34] with nSize =120000 completed in 28332002300 ns bubbleSort_Asc[35] with nSize =130000 completed in 33975997500 ns bubbleSort_Asc[36] with nSize =140000 completed in 38538996400 ns bubbleSort_Asc[37] with nSize =150000 completed in 44851976700 ns bubbleSort_Asc[38] with nSize =160000 completed in 51201999900 ns bubbleSort_Asc[39] with nSize =170000 completed in 57913993300 ns bubbleSort_Asc[40] with nSize =180000 completed in 64625002800 ns
5.5 Quick Sort Test
In this step, I will create a QuickSortTest to test sortAsc. It extends from TestBase and executes the test repeatedly for various inputs.
QuickSortTest.java
package org.jcg.zheng.sort;
import java.util.Collection;
import org.jcg.zheng.Utils;
import org.junit.Before;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runners.Parameterized;
@RunWith(Parameterized.class)
public class QuickSortTest extends TestBase {
@Parameterized.Parameters
public static Collection input() {
return TEST_SIZE_PARAMETER;
}
private QuickSort testClass;
public QuickSortTest(int nSize) {
super();
this.nSize = nSize;
}
@Test
public void quickSort_Asc() {
testClass.sortAsc(integerArray);
}
@Before
public void setup() {
testClass = new QuickSort();
this.filename = Utils.QUICK_SORT_TIME;
super.setup();
}
}
Output
quickSort_Asc[0] with nSize =10 completed in 0 ns quickSort_Asc[1] with nSize =200 completed in 0 ns quickSort_Asc[2] with nSize =300 completed in 999400 ns quickSort_Asc[3] with nSize =500 completed in 996500 ns quickSort_Asc[4] with nSize =800 completed in 0 ns quickSort_Asc[5] with nSize =1000 completed in 0 ns quickSort_Asc[6] with nSize =2000 completed in 1000100 ns quickSort_Asc[7] with nSize =3000 completed in 997600 ns quickSort_Asc[8] with nSize =4000 completed in 0 ns quickSort_Asc[9] with nSize =5000 completed in 1996000 ns quickSort_Asc[10] with nSize =6000 completed in 6996800 ns quickSort_Asc[11] with nSize =7000 completed in 996900 ns quickSort_Asc[12] with nSize =8000 completed in 998200 ns quickSort_Asc[13] with nSize =9000 completed in 1001100 ns quickSort_Asc[14] with nSize =10000 completed in 3996600 ns quickSort_Asc[15] with nSize =11000 completed in 2997400 ns quickSort_Asc[16] with nSize =12000 completed in 996700 ns quickSort_Asc[17] with nSize =13000 completed in 999200 ns quickSort_Asc[18] with nSize =14000 completed in 2001700 ns quickSort_Asc[19] with nSize =15000 completed in 1998900 ns quickSort_Asc[20] with nSize =16000 completed in 1992900 ns quickSort_Asc[21] with nSize =17000 completed in 1999200 ns quickSort_Asc[22] with nSize =18000 completed in 1999700 ns quickSort_Asc[23] with nSize =19000 completed in 1997700 ns quickSort_Asc[24] with nSize =20000 completed in 1997000 ns quickSort_Asc[25] with nSize =30000 completed in 2995800 ns quickSort_Asc[26] with nSize =40000 completed in 4994900 ns quickSort_Asc[27] with nSize =50000 completed in 5997100 ns quickSort_Asc[28] with nSize =60000 completed in 8000600 ns quickSort_Asc[29] with nSize =70000 completed in 8994500 ns quickSort_Asc[30] with nSize =80000 completed in 11001100 ns quickSort_Asc[31] with nSize =90000 completed in 10000500 ns quickSort_Asc[32] with nSize =100000 completed in 12998200 ns quickSort_Asc[33] with nSize =110000 completed in 14002600 ns quickSort_Asc[34] with nSize =120000 completed in 12999900 ns quickSort_Asc[35] with nSize =130000 completed in 12998300 ns quickSort_Asc[36] with nSize =140000 completed in 28001900 ns quickSort_Asc[37] with nSize =150000 completed in 17994100 ns quickSort_Asc[38] with nSize =160000 completed in 18002000 ns quickSort_Asc[39] with nSize =170000 completed in 19994400 ns quickSort_Asc[40] with nSize =180000 completed in 21002300 ns
5.6 Sorting Test Suite
In this step, I will create a SortsTestSuite class which includes SelectionSortTest, InsertionSortTest, BubbleSortTest, and QuickSortTest class. It will draw a graph to show the execution time relates to the input size for each algorithm.
SortsTestSuite.java
package org.jcg.zheng.sort;
import org.jcg.zheng.LineGraphChart;
import org.junit.AfterClass;
import org.junit.runner.RunWith;
import org.junit.runners.Suite;
import org.junit.runners.Suite.SuiteClasses;
@RunWith(Suite.class)
@SuiteClasses({ SelectionSortTest.class, InsertionSortTest.class, BubbleSortTest.class, QuickSortTest.class })
public class SortsTestSuite {
@AfterClass
public static void tearDown() {
LineGraphChart demo = new LineGraphChart("Sorting - Big O");
demo.pack();
demo.setVisible(true);
System.out.println("Done");
}
}
Execute it and captures the line graph here.
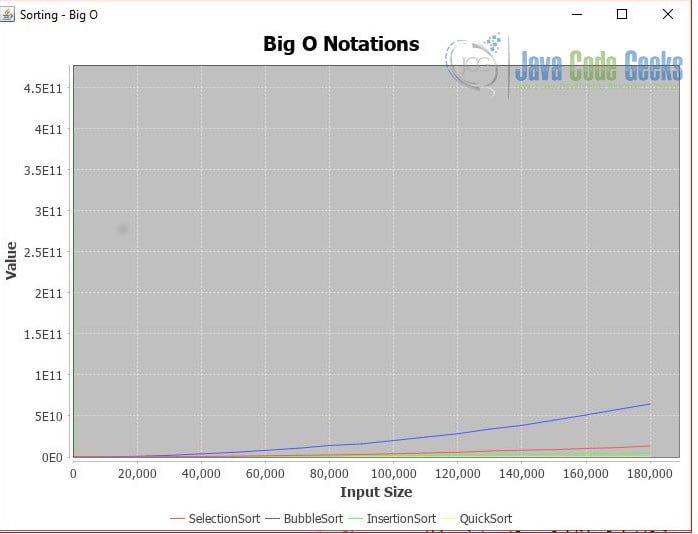
As you saw there, the selection sort performs better than the bubble sort but slower than the insertion sort and quick sort on the larger list.
5.7 Selection Sort Stability Test
In this step, I will create SelectionSortPojoTest to demonstrate the stability of algorithm. The selection sort is not stable as it doesn’t keep the original order if the two items compares same.
SelectionSortPojoTest.java
package org.jcg.zheng.sort;
import static org.junit.Assert.assertEquals;
import java.util.Arrays;
import org.jcg.zheng.Card;
import org.junit.Before;
import org.junit.Test;
public class SelectionSortPojoTest {
private Card[] cards = new Card[5];
private SelectionSortPojo testClass = new SelectionSortPojo();
@Before
public void setup() {
cards[0] = new Card("Heart", 10);
cards[1] = new Card("Diamond", 9);
cards[2] = new Card("Diamond", 10);
cards[3] = new Card("Heart", 9);
cards[4] = new Card("Spade", 1);
}
@Test
public void sortAsc() {
System.out.println("Before Sort " + Arrays.toString(cards));
testClass.sortAsc(cards);
System.out.println("After Sort " + Arrays.toString(cards));
assertEquals("Spade", cards[0].getColor());
assertEquals("Diamond", cards[1].getColor());
assertEquals("Heart", cards[2].getColor());
assertEquals("Heart", cards[3].getColor());
assertEquals("Diamond", cards[4].getColor());
}
}
Execute and capture the output here.
Before Sort [Card [color=Heart, number=10], Card [color=Diamond, number=9], Card [color=Diamond, number=10], Card [color=Heart, number=9], Card [color=Spade, number=1]] After Sort [Card [color=Spade, number=1], Card [color=Diamond, number=9], Card [color=Heart, number=9], Card [color=Diamond, number=10], Card [color=Heart, number=10]] org.junit.ComparisonFailure: expected:<[Heart]> but was:<[Diamond]> at org.junit.Assert.assertEquals(Assert.java:115) at org.junit.Assert.assertEquals(Assert.java:144) at org.jcg.zheng.sort.SelectionSortPojoTest.sortAsc(SelectionSortPojoTest.java:34)
6. Selection Sort Java Example – Summary
In this example, we explained the SelectionSort logic and compared it to InsertionSort, BubbleSort, and QuickSort. The time complexity is O(n^2) for all four algorithms. The InsertionSort, BubbleSort, and SelectionSort have space complexities of O(1). The QuickSort‘s space complexity is O(log n).
| Time Complexity | Space Complexity | Stability | |
| Selection Sort | O(n^2) | O(1) | No |
| Insertion Sort | O(n^2) | O(1) | Yes |
| Bubble Sort | O(n^2) | O(1) | Yes |
| Quick Sort | O(log n) | O(log n) | No |
As you saw in the chart, SelectionSort performs well on a small list, it’s better than BubbleSort on a larger list.
7. Download the Source Code
This example consists of a Maven project which shows the selection sort in Java in detail.
You can download the full source code of this example here: Selection Sort Java Example



I found this article very good. I have adapted it for my Advanced Java course to compare these four sorting techniques. I had a problem with the SortsTestSuite. It worked fine in IntelliJ, but would not run in Spring Tool Suite (Eclipse). I finally resolved the problem by removing the tearDown method from SortsTestSuite and into the TestBase class. The JUnit test suite class appears to have to be empty. Also, I have moved all of the common code from the four sort test classes to the TestBase class.
Thank you for the concept and the initial code.