Recursion Java Example

Aldo ZiflajSeptember 18th, 2014Last Updated: July 6th, 2022

0 695 5 minutes read

In this post, we will see multiple Recursion Examples in Java using recursive methods.

Recursion is a method of solving a problem, where the solution is based on “smaller” solutions of the same problem. In most programming languages (including Java) this is achieved by a function that calls itself in its definition. As a recursive joke says, “In order to understand recursion, you must firstly understand recursion”.

There are also other languages that are heavily based on recursion. This kind of languages, like Prolog, use recursion to solve every looping problem, without using iterative structures like for, while and/or do-while (there are no such structures in Prolog).

There is more than one type of recursion. In this example, I will show only some of them.

You can also check this tutorial in the following video:

1. Single Recursion Java Example

One type of recursion is single recursion, which means that the function calls itself only once. This recursion contains only a single self-reference in its implementation. It is best for list traversal such as linear search and factorial computation. Consider this example of calculating the factorial:

SingleRecursion.java

package com.javacodegeeks.examples;
 
import java.util.Scanner;
 
public class SingleRecursion {
 
    public static long factorial(int n) {
        if (n<0) throw new IllegalArgumentException("Can't calculate factorial of negative");
        return (n<2) ? 1 : n*factorial(n-1);
    }
     
    public static void main(String[] args) {
        Scanner stdIn = new Scanner(System.in);
        System.out.print("Factorial of what number do you want to calculate? ");
        int num = stdIn.nextInt();
        System.out.printf("%d! = %d", num, factorial(num));
 
        stdIn.close();
    }
     
}

Based on the definition of the factorial, which states that 0!=1, 1!=1, and n! = n * (n-1)!, I wrote this function which uses the same formula to calculate the factorial.

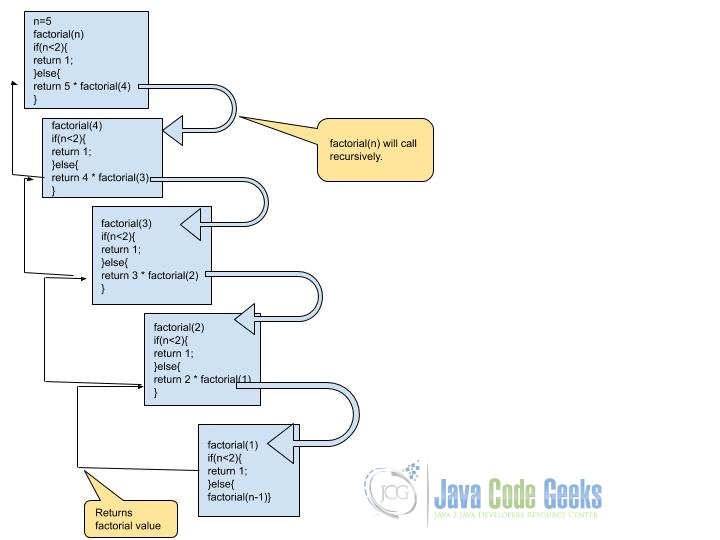
Recursion Java - recursive - Diagram — Diagram

For an input of 5, it follows this workflow:

Firstly, calls 5 = 5 * 4! , then 4! = 4 * 3!, then 3! = 3 * 2!, and 2! = 2 * 1!
It knows that 1! = 1 , since for every integer smaller than 2 (i.e. 0 and 1) is 1
Based on this, it calculates 2! = 2 , 3! = 3 * 2 = 6 , 4! = 4 * 6 = 24 and finally 5! = 5 * 24 = 120
Returns the final result, which is 120

And the output of this is:

Factorial of what number do you want to calculate? 5
5! = 120

That is the simplest case of single recursion. Other use cases are the Euclidean algorithm for finding the Greatest Common Divisor, the binary search algorithm, etc.

2. Multiple Recursion

Another type of recursion is multiple recursion, which means that the function calls itself more than once. This recursion contains only a multi self-reference in its implementation. It is best for tree traversal such as depth – first search and Fibonacci sequence computation. Consider this example of generating the Fibonacci sequence:

MultipleRecursion.java

package com.javacodegeeks.examples;
 
import java.util.Scanner;
 
public class MultipleRecursion {
 
    public static long fibonacci(long n) {
        if (n<0) throw new IllegalArgumentException("Can't accept negative arguments");
        return (n < 2) ? n : fibonacci(n-1) + fibonacci(n-2);
    }
     
    public static void main(String[] args) {
        Scanner stdIn = new Scanner(System.in);
         
        System.out.print("How many numbers do you want to print? ");
        int iter = stdIn.nextInt();
        for (int i=0;i<iter;i++) {
            System.out.print(fibonacci(i) + " ");
        }
         
        stdIn.close();
 
    }
 
}

If you check on line 9, the function calls itself twice to calculate the value that should return. You should know that each call to a recursive function gets its own copy of variables, so the both function calls don’t affect each other. One sample output of this is:

How many numbers do you want to print? 10
0 1 1 2 3 5 8 13 21 34 

Of course, sometimes the multiple recursion can be converted to single recursion, and also in iteration.

3. Mutual Recursion

Mutual (or indirect) recursion is when the first function calls a second one, and this second one calls the first one. Of course, there are scenarios with more than two functions.

To see an example of mutual recursion, consider the following code:

MutualRecursion.java

package com.javacodegeeks.examples;
 
import java.util.Scanner;
 
public class MutualRecursion {
     
    public static boolean isOdd(int n) {
        if (n<0) throw new IllegalArgumentException("Can't accept negative arguments");
        return (n == 0) ? false : isEven(n-1);
    }
     
    public static boolean isEven(int n) {
        if (n<0) throw new IllegalArgumentException("Can't accept negative arguments");
        return (n == 0) ? true : isOdd(n-1);
    }
     
    public static void main(String[] args) {
        Scanner stdIn = new Scanner(System.in);
        System.out.print("Enter a number: ");
        int num = stdIn.nextInt();
         
        if (isEven(num)) System.out.println(num + " is even");
        else System.out.println(num + " is odd");
         
        stdIn.close();
    }
 
}

In this example, you can see that a function call like isEven(3) is equivalent to isOdd(2), which by the way is equivalent to isEven(1), which is finally equivalent to isOdd(0). This happens with every other argument passed to any of the functions, it gets reduced to 0.

For the number 3, the output is:

Enter a number: 3
3 is odd

4. Tail recursion

If you recall the single recursion example about the factorial, you may notice than firstly it calculates the factorials of numbers from 1 to the required number. That means, your calculations are done after every other calculation is done.

Tail recursion does the same opposite of this; it makes your calculations, then it passes the result to the other call, until the result is calculated. In functional programming languages that don’t use normal iteration, the tail recursion (also known as tail call) becomes equivalent to loops.

To see how tail recursion is used, see this example:

TailRecursion.java

package com.javacodegeeks.examples;
 
import java.util.Scanner;
 
public class TailRecursion {
 
    public static int tailFactorial(int n, Object... previous) {
        if (n 0) ? (int) previous[0] : 1;
         
        return (n < 2) ? prev : tailFactorial(n-1,n*prev);
    }
     
    public static void main(String[] args) {
        Scanner stdIn = new Scanner(System.in);
        System.out.print("Factorial of what number do you want to calculate? ");
        int num = stdIn.nextInt();
        System.out.printf("%d! = %d", num, tailFactorial(num));
         
        stdIn.close();
    }
}

The tailFactorial() method does the same thing as the factorial() method on the single recursion example, but it uses tail recursion. The output is the same as before:

Factorial of what number do you want to calculate? 5
5! = 120

5. Problems with recursion

Of course, recursion is a very clever solution to a problem, and it is heavily used in divide-and-conquer algorithms. But every coin has two sides, and the other side of recursion is stack overflow.

To witness the stack overflow, consider this simple example:

StackOverflow.java

package com.javacodegeeks.examples;
 
public class StackOverflow {
    public static void recursive(int num) {
        System.out.println(num);
        recursive(num+1);
    }
     
    public static void main(String[] args) {
        recursive(1);
    }
 
}

After the recursive method prints the argument, it calls itself with a bigger argument and this is repeated infinitely. After the recursive method was called 11407 times, it gave this output:

Exception in thread "main" java.lang.StackOverflowError
    at java.io.PrintStream.write(Unknown Source)
    at sun.nio.cs.StreamEncoder.writeBytes(Unknown Source)
    at sun.nio.cs.StreamEncoder.implFlushBuffer(Unknown Source)
    at sun.nio.cs.StreamEncoder.flushBuffer(Unknown Source)
    at java.io.OutputStreamWriter.flushBuffer(Unknown Source)
    at java.io.PrintStream.write(Unknown Source)
    at java.io.PrintStream.print(Unknown Source)
    at java.io.PrintStream.println(Unknown Source)
    at com.javacodegeeks.examples.StackOverflow.recursive(StackOverflow.java:5)
    at com.javacodegeeks.examples.StackOverflow.recursive(StackOverflow.java:6)

6. Download the Source Code

That was an example of Recursion in Java.

Download
You can download the full source code of this example here: Recursion Java Example

Last updated on Feb. 24th, 2020

Recursion Java Example

1. Single Recursion Java Example

2. Multiple Recursion

3. Mutual Recursion

4. Tail recursion

5. Problems with recursion

6. Download the Source Code

Thank you!

Aldo Ziflaj

Thank you!

1. Single Recursion Java Example

2. Multiple Recursion

3. Mutual Recursion

4. Tail recursion

5. Problems with recursion

6. Download the Source Code

Thank you!

Related Articles

Thank you!