Quicksort Java algorithm – Code Example
In this article, we will discuss the implementation of Quicksort Java algorithm. Quicksort is the most widely used sorting algorithm. Quick sort is faster than most other common sorting algorithms. It was developed by the famous Computer Scientist Tony Hoare and it is based on the Divide and Conquer Algorithm.
First, we are going to explain how Quick sort works on an algorithmic level, with some simple examples. Finally, we will build our implementation in Java and discuss its performance.
You can also check this tutorial in the following video:
1. The Quicksort Java Algorithm
Quick sort works recursively in order to sort a given array. These are the three basic steps of the Quicksort algorithm:
1. Partition the array into left and right sub-arrays, in which the items in the left sub-array are smaller than the specified item and the items in the right sub-array are greater than the specified item.
2. Recursively call the Quicksort to sort the left sub-array.
3. Recursively call the Quicksort to sort the right sub-array.

The partitioning step is the key when sorting an array with Quicksort. Quicksort itself uses a Partition algorithm to partition the given array.
The partition works by using two cursors (let say), one at each end of the array. These cursors move towards each other. If the left cursor finds an item that is smaller than the pivot value, it ignores it and moves forward. But if the item’s value is greater than the pivot value, it stops. Similarly for the right cursor, if an item is greater than the pivot value it ignores it and moves backward, else the cursor stops. When both cursors stop, the items pointed by the cursors get swapped. That’s because these items are on the wrong side of the array. After the swap, both the cursors continue, and stop at the items which are on the wrong side of the array and swap them. And that’s how the algorithm goes on until finally all items are sorted.
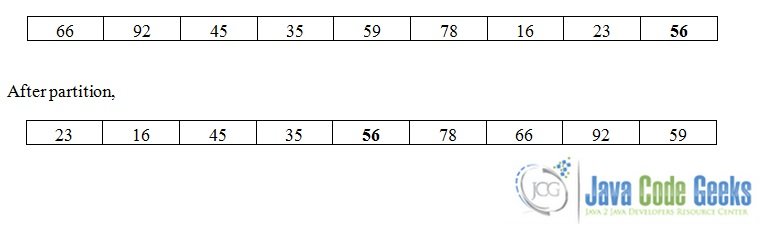
The pivot value is the value that is used to partition the array into two sub-arrays. After the partition, the items in the left sub-array are smaller than the pivot value, and the items in the right sub-array are greater than the pivot value.
In the above figure, we chose 56 as a pivot value. After the partition (which of course consists of more than one sub-steps), all the items on the left of the pivot are smaller, and the items on the right of it are greater than it and the pivot is at its sorted position. Also notice that, at this point, the array is not sorted of course. That was just one partitioning step.
You can choose any random value from the array as a pivot value. Later we will see that choosing a pivot value affects the performance of the algorithm. But for now, lets us take the rightmost item of the array as a pivot value and attempt to create the first version of our Java implementation.
QuicksortExample.java
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 | package com.javacodegeeks.sorting.quicksort;public class QuicksortExample { private static int []a; public static void main(String[] args) { // Get a random generated array a = getArray(); // prints the given array printArray(); // sort the array sort(); System.out.println(""); //prints the sorted array printArray(); } // This method sorts an array and internally calls quickSort public static void sort(){ int left = 0; int right = a.length-1; quickSort(left, right); } // This method is used to sort the array using quicksort algorithm. // It takes the left and the right end of the array as the two cursors. private static void quickSort(int left,int right){ // If both cursor scanned the complete array quicksort exits if(left >= right) return; // For the simplicity, we took the right most item of the array as a pivot int pivot = a[right]; int partition = partition(left, right, pivot); // Recursively, calls the quicksort with the different left and right parameters of the sub-array quickSort(0, partition-1); quickSort(partition+1, right); } // This method is used to partition the given array and returns the integer which points to the sorted pivot index private static int partition(int left,int right,int pivot){ int leftCursor = left-1; int rightCursor = right; while(leftCursor < rightCursor){ while(a[++leftCursor] < pivot); while(rightCursor > 0 && a[--rightCursor] > pivot); if(leftCursor >= rightCursor){ break; }else{ swap(leftCursor, rightCursor); } } swap(leftCursor, right); return leftCursor; } // This method is used to swap the values between the two given index public static void swap(int left,int right){ int temp = a[left]; a[left] = a[right]; a[right] = temp; } public static void printArray(){ for(int i : a){ System.out.print(i+" "); } } public static int[] getArray(){ int size=10; int []array = new int[size]; int item = 0; for(int i=0;i<size;i++){ item = (int)(Math.random()*100); array[i] = item; } return array; }} |
If we run the above code, we will have the following results:
1 2 | 4 94 87 24 44 30 37 97 47 93 4 24 30 37 44 47 87 93 94 97 |
Let’s discuss how the above program works.
The quickSort() method takes two parameters, each holding the position of the cursors at the two ends of an array or a sub-array that needs to be sorted. For example, if left = 3, then the left cursor points to element 3 of the array. The method exits, if left is greater than or equal to right, which means that the array is already sorted or the length of the array is one. It also generates a pivot value, in this case, the rightmost value of the array. The pivot value is passed to the partition method which is used to partition the given array.
The partition() method scans the array and swaps the items which are not at their proper place. The items which are greater than the pivot value, are swapped to the right of the pivot value with the values which are smaller than the pivot value. At the end of each scan, the left cursor ends up pointing to the left element of the right sub-array. The pivot is then swapped with it and puts it into its proper sorted place. This method returns an integer that is the position of the sorted pivot value that partitioned the given array or a sub-array.
Then, the quicksort() method spawns the recursive call to sort the left sub-array and the right sub-array. Let’s have a deeper look into the partition method.
int leftCursor = left-1; : This statement initializes a leftCursor to one less than the left parameter. This is because while scanning, it first gets incremented and then used to evaluate. For example, if we are scanning the complete array and not a sub-array, the leftCursor will be at 0-1, i.e., -1.
int rightCursor = right; : This statement initializes a rightCursor to the right end of the given array, i.e., rightCursor = array.lenght-1.
while(leftCursor < rightCursor): The outer while loop runs till the leftCursor is not in the same position or a position greater than the rightCursor. When this condition evaluates to false, it means that the cursors have scanned the complete array.
while(a[++leftCursor] < pivot);: This inner while loop has nothing inside its body. It’s used to move the left cursor towards the right and compare the item it’s pointing with the pivot. The loop terminates if the pointed value is greater than the pivot value.
while(rightCursor > 0 && a[--rightCursor] > pivot);: This loop does a similar work. It moves towards the left of the array and compares each item it points with the pivot. If the pointed value is smaller than the pivot value, it terminates.
When both inner while loops terminate, both the cursors point to the items which are not at their proper place. We first check whether the cursors have crossed each other, which means they have scanned the full array. Then, it exits from the loop, else the items get swapped.
Then, the quicksort() method is called recursively. This time with the two sub-arrays, the left one starting from partition-1, and the right one starting from partition+1. It sorts the sub-arrays, until the full array gets partitioned and sorted, which finally results in the full sorted array.
Generally, quick sort operates in O(nlog n) time. But there are some cases when its performance degrades to O(n2). The problem lies in the selection of the pivot. In the above example, we choose the pivot randomly (the rightmost item of the array). The pivot should be the median of the items to be sorted. So, half of the items in the array should be smaller than the pivot, and the rest should be larger than the pivot. This would result in two equally sized sub-arrays. This is the best situation for the Quicksort algorithm, where it runs at O(nlogn). Having one large and one small sub-array results in less efficiency.
2. Median of 3 Partitioning
Regarding the quicksort algorithm, the best approach to choose a pivot is by choosing the median of the first, middle, and the last items of the array. This approach is known as the ‘median-of-three’ approach.
QuicksortMedianExample.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067 068 069 070 071 072 073 074 075 076 077 078 079 080 081 082 083 084 085 086 087 088 089 090 091 092 093 094 095 096 097 098 099 100 101 102 103 104 105 | package com.javacodegeeks.sorting.quicksort;public class QuicksortMedianExample { private static int []a; public static void main(String[] args) { // Get a random generated array a = getArray(); // prints the given array printArray(); // sort the array sort(); System.out.println(""); //prints the sorted array printArray(); } // This method sorts an array and internally calls quickSort public static void sort(){ int left = 0; int right = a.length-1; quickSort(left, right); } // This method is used to sort the array using quicksort algorithm. // It takes left and the right end of the array as two cursors private static void quickSort(int left,int right){ // If both cursor scanned the complete array, quicksort exits if(left >= right) return; // Pivot using median of 3 approach int pivot = getMedian(left, right); int partition = partition(left, right, pivot); // Recursively, calls the quicksort with the different left and right parameters of the sub-array quickSort(0, partition-1); quickSort(partition+1, right); } // This method is used to partition the given array and returns the integer which points to the sorted pivot index private static int partition(int left,int right,int pivot){ int leftCursor = left-1; int rightCursor = right; while(leftCursor < rightCursor){ while(a[++leftCursor] < pivot); while(rightCursor > 0 && a[--rightCursor] > pivot); if(leftCursor >= rightCursor){ break; }else{ swap(leftCursor, rightCursor); } } swap(leftCursor, right); return leftCursor; } public static int getMedian(int left,int right){ int center = (left+right)/2; if(a[left] > a[center]) swap(left,center); if(a[left] > a[right]) swap(left, right); if(a[center] > a[right]) swap(center, right); swap(center, right); return a[right]; } // This method is used to swap the values between the two given index public static void swap(int left,int right){ int temp = a[left]; a[left] = a[right]; a[right] = temp; } public static void printArray(){ for(int i : a){ System.out.print(i+" "); } } public static int[] getArray(){ int size=10; int []array = new int[size]; int item = 0; for(int i=0;i<size;i++){ item = (int)(Math.random()*100); array[i] = item; } return array; }} |
If we run the above code, we will have the following results:
1 2 | 80 4 33 30 65 14 35 25 31 12 4 12 14 25 30 31 33 35 65 80 |
In the above example, we have used the median-of-3 approach to find a “good” pivot. We used the first, the middle, and last items of the array to find the median. The median is the middle item between the orderly placed items. This approach is not only used to select the pivot but also to put the three items in their sorted place in the array. Let us look at getMedian() in the above example.
getMedian(int left, int right): This method is used to return a median among the three items specified. The returned median is used as the pivot in quicksort. This method has two parameters, both pointing at each end of the array or the sub-array. We used the middle, left and right items to find the median. In the end, we swapped the median with the item at the rightmost position of the array. So, after the scan, all these three items should be in their proper sorted places in the array. This process is repeated with all the sub-arrays having different left, right and middle positions until the full array gets sorted.
3. Quick sort with String
So far, we have seen quicksort with integer arrays. In this example, we will sort an array of Strings using quicksort.
QuicksortStringExample.java
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 | package com.javacodegeeks.sorting.quicksort;public class QuicksortStringExample { private static String []a; public static void main(String[] args) { // Get an String array a = new String[]{"X","E","C","A"}; // prints the given array printArray(); // sort the array sort(); System.out.println(""); //prints the sorted array printArray(); } // This method sort an array internally and internally calls quickSort public static void sort(){ int left = 0; int right = a.length-1; quickSort(left, right); } // This method is used to sort the array using quicksort algorithm. // It takes left and the right end of the array as two cursors private static void quickSort(int left,int right){ // If both cursor scanned the complete array quicksort exits if(left >= right) return; // Pivot using median of 3 approach String pivot = getMedian(left, right); int partition = partition(left, right, pivot); // Recursively, calls the quicksort with the different left and right parameters of the sub-array quickSort(0, partition-1); quickSort(partition+1, right); } // This method is used to partition the given array and returns the integer which points to the sorted pivot index private static int partition(int left,int right,String pivot){ int leftCursor = left-1; int rightCursor = right; while(leftCursor < rightCursor){ while(((Comparable<String>)a[++leftCursor]).compareTo(pivot) < 0); while(rightCursor > 0 && ((Comparable<String>)a[--rightCursor]).compareTo(pivot) > 0); if(leftCursor >= rightCursor){ break; }else{ swap(leftCursor, rightCursor); } } swap(leftCursor, right); return leftCursor; } public static String getMedian(int left,int right){ int center = (left+right)/2; if(((Comparable<String>)a[left]).compareTo(a[center]) > 0) swap(left,center); if(((Comparable<String>)a[left]).compareTo(a[right]) > 0) swap(left, right); if(((Comparable<String>)a[center]).compareTo(a[right]) > 0) swap(center, right); swap(center, right); return a[right]; } // This method is used to swap the values between the two given index public static void swap(int left,int right){ String temp = a[left]; a[left] = a[right]; a[right] = temp; } public static void printArray(){ for(String i : a){ System.out.print(i+" "); } } } |
If we run the above code, we will have the following results:
1 2 | X E C A A C E X |
In the above example, we sorted an array of Strings, using the quicksort. The String class implements the Comparable interface and overrides the compareTo() method. We used the compareTo() method to compare the Strings. We downcasted the String to the Comparable type and used the compareTo() method to find the greater or the smaller between them.
The comparison is done using the natural ordering of the String. The natural ordering in String is maintained alphabetically from A – Z and then from a – z. The rest of the code works the same as shown in the previous example.
4. Quicksort Objects
In this example, we will see how to sort Objects of a class using the Quicksort. We will create a generic quicksort method that can be used to sort objects of any class. The class needs to implement the Comparable interface and override the method compareTo in order to use the quicksort, otherwise, it will throw a ClassCastException.
Let’s create an Employee class and sort employees on the basis of their employeeCode using the quick sort.
Employee.java
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | package com.javacodegeeks.entity;public class Employee implements Comparable<Employee>{ private String firstName; private String lastName; private int emplyeeCode; public Employee(String fistName,String lastName,int emplyeeCode){ this.firstName = fistName; this.lastName = lastName; this.emplyeeCode = emplyeeCode; } public String getFirstName() { return firstName; } public void setFirstName(String firstName) { this.firstName = firstName; } public String getLastName() { return lastName; } public void setLastName(String lastName) { this.lastName = lastName; } public int getEmplyeeCode() { return emplyeeCode; } public void setEmplyeeCode(int emplyeeCode) { this.emplyeeCode = emplyeeCode; } public String toString(){ return "Employee Code: "+getEmplyeeCode()+", Name:"+getFirstName()+" "+getLastName(); } public int compareTo(Employee o) { Employee e = (Employee)o; if(this.emplyeeCode > e.getEmplyeeCode()) return 1; if(this.emplyeeCode < e.getEmplyeeCode()) return -1; if(this.emplyeeCode == e.getEmplyeeCode()) return 0; return 0; }} |
We created an Employee class that implements the Comparable interface and overrides the compareTo() method. The comparison between the Employee objects are defined by comparing the employeeCode property of the Employee objects. The comparTo() method returns an integer, which tells whether the current employeeCode is greater than, or smaller than or equal to the compared employeeCode. It returns 1 if the current employeeCode is greater than the compared employeeCode, -1 if, the current employeeCode is smaller than the compared employeeCode, else it returns 0 if both are equal. Since the employeeCode is of type integer, we have compared it using the simple integer comparison operators.
QuicksortObjectExample.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067 068 069 070 071 072 073 074 075 076 077 078 079 080 081 082 083 084 085 086 087 088 089 090 091 092 093 094 095 096 097 098 099 100 101 102 103 104 105 106 107 108 109 110 111 | package com.javacodegeeks.sorting.quicksort;import com.javacodegeeks.entity.Employee;public class QuicksortObjectExample<T extends Comparable<T>> { private T []a; public static void main(String[] args) { Employee []employees = new Employee[5]; Employee employee = new Employee("John","Carter",5658); employees[0] = employee; employee = new Employee("Mary","Carter",7412); employees[1] = employee; employee = new Employee("Alex","Lumb",1158); employees[2] = employee; employee = new Employee("David","Jhonson",1254); employees[3] = employee; employee = new Employee("Shaun","Smith",4587); employees[4] = employee; QuicksortObjectExample<Employee>ex = new QuicksortObjectExample<>(); // Assigned array ex.a = employees; // prints the given array ex.printArray(); // sort the array ex.sort(); System.out.println(""); //prints the sorted array ex.printArray(); } // This method sort an array and internally calls quickSort public void sort(){ int left = 0; int right = a.length-1; quickSort(left, right); } // This method is used to sort the array using quicksort algorithm. // It takes left and the right end of the array as two cursors private void quickSort(int left,int right){ // If both cursor scanned the complete array quicksort exits if(left >= right) return; // Pivot using median of 3 approach T pivot = getMedian(left, right); int partition = partition(left, right, pivot); // Recursively, calls the quicksort with the different left and right parameters of the sub-array quickSort(0, partition-1); quickSort(partition+1, right); } // This method is used to partition the given array and returns the integer which points to the sorted pivot index private int partition(int left,int right,T pivot){ int leftCursor = left-1; int rightCursor = right; while(leftCursor < rightCursor){ while(((Comparable<T>)a[++leftCursor]).compareTo(pivot) < 0); while(rightCursor > 0 && ((Comparable<T>)a[--rightCursor]).compareTo(pivot) > 0); if(leftCursor >= rightCursor){ break; }else{ swap(leftCursor, rightCursor); } } swap(leftCursor, right); return leftCursor; } public T getMedian(int left,int right){ int center = (left+right)/2; if(((Comparable<T>)a[left]).compareTo(a[center]) > 0) swap(left,center); if(((Comparable<T>)a[left]).compareTo(a[right]) > 0) swap(left, right); if(((Comparable<T>)a[center]).compareTo(a[right]) > 0) swap(center, right); swap(center, right); return a[right]; } // This method is used to swap the values between the two given index public void swap(int left,int right){ T temp = a[left]; a[left] = a[right]; a[right] = temp; } public void printArray(){ for(T i : a){ System.out.println(i+" "); } } } |
If we run the above code, we will have the following results:
01 02 03 04 05 06 07 08 09 10 11 | Employee Code: 5658, Name:John Carter Employee Code: 7412, Name:Mary Carter Employee Code: 1158, Name:Alex Lumb Employee Code: 1254, Name:David Jhonson Employee Code: 4587, Name:Shaun Smith Employee Code: 1158, Name:Alex Lumb Employee Code: 1254, Name:David Jhonson Employee Code: 4587, Name:Shaun Smith Employee Code: 5658, Name:John Carter Employee Code: 7412, Name:Mary Carter |
In the above example, we have created a generic class that can be used to sort any objects of any type, using quick sort. Any class T which implements the Comparable interface can be used. It performs the same functionality as shown in the previous example. The only difference is that this class is generic and it accepts any class T in its generic parameter which implements the Comparable interface.
In the previous code, we created the Employee class which implements Comparable interface and provides its own rule on how to compare its objects. The above class creates an array of the Employee class and assigns it to the array a. We print to show the current unsorted array of objects. Then, we called the sort() method which sorted the array of Employee type.
Please note that the comparison of the objects of the type Employee, is done by the rule defined in the compareTo() method in the Employee class i.e. on the basis of the employeeCode property of the class.
4. Complexity and comparison with other sorting techniques
As we noticed earlier, the Quicksort algorithm works well when the pivot is in the middle. The best case is O(nlogn) and the worst case would be O(n2). Let us now check how it fares against the other sorting techniques. Comparison is usually done based on time and space complexity.
- Bubble Sort: This simplest sorting technique works by iterating through the array and comparing each element. The complexity in best and worst cases is O(n2).
- Selection Sort: In this technique, elements are selected and placed in sorted order. Similar to Bubble sort, the best and worst-case complexity is O(n2).
- Insertion Sort: In this technique, each element of the array is inserted in the proper position. The best case would be when the array is already sorted. The best case would take O(n) and the worst case would be O(n2). This is best suitable when we have a small array to sort.
- Quick Sort: Quick Sort, as we saw, would take O(nlogn) for the best case when the right pivot is chosen. The worst case is when the array is already sorted or reverse sorted. The complexity in such a scenario would be O(n2). This is an in-place sorting mechanism and hence is space-efficient.
- Merge Sort: Like Quick Sort, this is also a divide and conquer recursive mechanism. The best, worst and average case for this mechanism is O(nlogn). But the sorting doesn’t happen in-place and hence is not space-efficient.
- Heap Sort: This in-place sorting mechanism has best, worst and average complexity as O(nlogn).
| Sorting mechanism | Best case | Average case | Worst case |
| Bubble Sort | O(n2) | O(n2) | O(n2) |
| Selection Sort | O(n2) | O(n2) | O(n2) |
| Insertion Sort | O(n) | O(n2) | O(n2) |
| Quick Sort | O(nlogn) | O(nlogn) | O(n2) |
| Merge Sort | O(nlogn) | O(nlogn) | O(nlogn) |
| Heap Sort | O(nlogn) | O(nlogn) | O(nlogn) |
5. Download the source code
This was an example on Quicksort algorithm in Java.
You can download the source code of this example from here: Quicksort Java algorithm – Code Example
Last updated on Feb. 12th, 2020





Hey, thank you very much for your help, just some debugging for one of the parts. In the “2. Median of 3 Partitioning” approach you are making a mistake. On line 44 “quickSort(0, partition-1);” you should actually be doing “quickSort(left, partition-1);” because as it stands you are always trying to sort from the beginning of the array and makes it really really wrong. Once that is fixed it runs properly again though, so you should consider fixing it for any people looking at your code in the future.
Again, thanks for your help.
He’s right you know ^^… the algorithm will still sort, but will re-examine already sorted sections of the array with every recursive call to quick sort — which becomes extremely inefficient the larger the array size is. Even for sizes of 75-100 it will take several minutes. While with the adjustment, it runs almost instantly on my machine for an array of size 100000. helluva difference.
Hope you don’t put this on your CV ;)