Math.pow Java Example
In this article, we examine the Math.pow Java method so as to use exponents in java and we provide some examples of its use.
1. Introduction
The java.lang package provides classes and interfaces that are central to the Java programming language. The Math class from the java.lang package contains static methods for performing many common math operations. In java, these include exponents, logarithm, square root, and trigonometric functions.
One such method is Math::pow and helps us to deal with exponents in java. This method calculates and returns the result of a base number raised to the power of the exponent. The signature of the method is double pow(double a, double b), where the first argument is the base number and the second number is the exponent. For example, 2 raised to the power of 3 (2^3) can be calculated with the following method call: Math.pow(2, 3)
(Note that 2^3 will perform an exclusive OR bitwise operation. Bitwise logical operators such as ^ compare the binary representations of integral types.)
The calculated result must be within 1 ULP (Unit in the Last Place) of the exact result. (For an explanation of Unit in the Last Place, visit https://programmingwords.com/home/ulp-machine-epsilon.)
There are some special cases that apply when using Math::pow. They are covered in the example below.
1.1 Tools Used in this Example
- Eclipse IDE for Enterprise Java Developers Version: 4.11.0
- JUnit Version 4.12
2. Java Math.pow Example
2.1 Create the JUnit Maven Project
Let’s create a simple Maven Project for our JUnit tests. Select “New” -> Maven Project” and select the “Create a simple project (skip archetype selection)” checkbox and click “Next”.
Enter a Group Id, Artifact Id, and select “jar” for Packaging and click “Finish”.
Open the pom.xml file and add the following just below the versionelement.
pom.xml
<project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd"> <modelVersion>4.0.0</modelVersion> <groupId>com.javacodegeeks.examples</groupId> <artifactId>math-power-test</artifactId> <version>0.0.1-SNAPSHOT</version> <build> <plugins> <plugin> <groupId>org.apache.maven.plugins</groupId> <artifactId>maven-compiler-plugin</artifactId> <version>3.8.0</version> <configuration> <source>1.8</source> <target>1.8</target> </configuration> </plugin> </plugins> </build> <dependencies> <dependency> <groupId>junit</groupId> <artifactId>junit</artifactId> <version>4.12</version> </dependency> </dependencies> </project>
The maven-compiler-plugin will be used for building the project. The compiler is configured for Java SE 8. We also added the JUnit dependency.
Save the changes and select Maven->Update Project from the project context menu. Select your project from “Available Maven Codebases”. Leave the other defaults and click OK.
2.2 Create Math::pow Test Case
Right-click the /scr/test/java folder and select New > Other… JUnit Test Case. Click Next. Enter com.javacodegeeks.examples for the package name and “MathPowTest” for the test case name. Leave the other default values and click Finish
Add the following code to the MathPowTest class.
MathPowTest.java
import static org.junit.Assert.assertTrue;
import org.junit.Test;
public class MathPowTest {
@Test
public void range() {
System.out.println("\n**** range ****");
int base = 2;
for (int exponent = 0; exponent <= 16; exponent++) {
System.out.println(
String.format("%d^%d = %,d",
base,
exponent,
(int) Math.pow(base, exponent)));
}
}
@Test
public void fpCalc() {
System.out.println("\n**** fpCalc ****");
double result = Math.pow(2.21, 2);
System.out.println("Math.pow(2.21, 2) = " + result);
assertTrue(result == 4.8841);
}
@Test
public void fractionalExponent() {
System.out.println("\n**** fractionalExponent ****");
System.out.println(Math.pow(8, 1/3));
double oneThird = (double) 1/3;
double result = Math.pow(8, oneThird);
System.out.println("Math.pow(8, oneThird) = " + result);
assertTrue(result == 2);
}
@Test
public void productOfPowers() {
System.out.println("\n**** productOfPowers ****");
double base = 2;
double exp1 = 2;
double exp2 = 3;
double res1 = Math.pow(base, exp1);
double res2 = Math.pow(base, exp2);
System.out.println("result 1: " + res1);
System.out.println("result 2: " + res2);
double res3 = Math.pow(base, exp1 + exp2);
System.out.println("result 3: " + res3);
assertTrue(res1 * res2 == res3);
}
}
The first test method, range, does not actually test anything but rather prints out the results of raising the base number 2 to the power of 0 through 16. (We cast the results as int values in order to display them as integers instead of double values.)
The second method, fpCalc,
calls the Math.pow method with two
arbitrary arguments (the base being a floating point number) and asserts the
result.
The third method, fractionalExponent,
requires the casting of 1/3 to a double type in order to calculate the result correctly. If we use Math.pow(8, 1/3), integer arithmetic (division) is used and the result will be incorrect.
The last method, productOfPowers, tests the “product of powers” property. This algebraic rule states that when multiplying two powers with the same base you can add the exponents to simplify the equation.
Right-click the test class and select Run As > JUnit Test. The result is shown below.
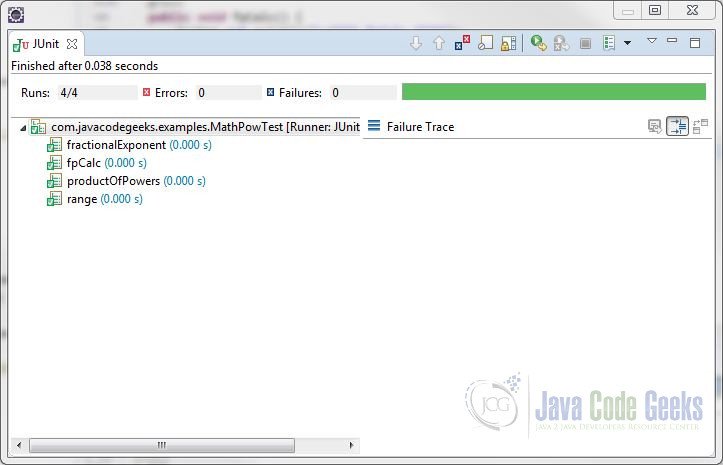
You will also see the following output in the console.
JUnit Test Output
**** fractionalExponent **** 1.0 Math.pow(8, oneThird) = 2.0 **** fpCalc **** Math.pow(2.21, 2) = 4.8841 **** productOfPowers **** result 1: 4.0 result 2: 8.0 result 3: 32.0 **** range **** 2^0 = 1 2^1 = 2 2^2 = 4 2^3 = 8 2^4 = 16 2^5 = 32 2^6 = 64 2^7 = 128 2^8 = 256 2^9 = 512 2^10 = 1,024 2^11 = 2,048 2^12 = 4,096 2^13 = 8,192 2^14 = 16,384 2^15 = 32,768 2^16 = 65,536
Note that the test execution order is not predictable.
2.3 Special Cases
The following table shows the return value for various special cases for exponents in java, where ‘a’ is the first argument (the base number) and ‘b’ is the second argument (the exponent). Note that NaN is the symbol for “not a number”.
(The case numbers are used for reference only and are not part of an official designation.)
Special Cases Table
| Case | Arguments | Return Value |
| 1 | a or b = NaN. | NaN |
| 2 | a = Any value except NaN; b = 0. | 1 |
| 3 | a = NegativeInfinity; b < 0. | 0 |
| 4 | a = NegativeInfinity; b is a positive odd integer. | NegativeInfinity |
| 5 | a = NegativeInfinity; b is positive but not an odd integer. | PositiveInfinity |
| 6 | a < 0 but not NegativeInfinity; b is not an integer, NegativeInfinity, or PositiveInfinity. | NaN |
| 7 | a = -1; b = NegativeInfinity or PositiveInfinity. | NaN |
| 8 | -1 < a < 1; b = NegativeInfinity. | PositiveInfinity |
| 9 | -1 < a < 1; b = PositiveInfinity. | 0 | 10 | a 1; b = NegativeInfinity. | 0 | 11 | a 1; b = PositiveInfinity. | PositiveInfinity | 12 | a = 0; b < 0. | PositiveInfinity | 13 | a = 0; b > 0. | 0 | 14 | a = 1; b is any value except NaN. | 1 | 15 | a = PositiveInfinity; b < 0. | 0 | 16 | a = PositiveInfinity; b > 0. | PositiveInfinity |
We will look at examples for each special case included in the table.
Create a new JUnit test case under /scr/test/java . Enter “SpecialCasesTest” for the test case name.
Add the following code to the SpecialCasesTest class.
SpecialCasesTest.java
import static org.junit.Assert.*;
import org.junit.Test;
public class SpecialCasesTest {
@Test
public void aOrbEqNaN() {
System.out.println("\n**** aOrbEqNaN ****");
// 1. If the first argument is NaN then the result is NaN.
System.out.println(Math.pow(Double.NaN, 2));
assertTrue(Double.isNaN(Math.pow(Double.NaN, 2)));
// 1. If the second argument is NaN then the result is NaN.
System.out.println(Math.pow(2, Double.NaN));
assertTrue(Double.isNaN(Math.pow(2, Double.NaN)));
}
@Test
public void aEqAnyAndbEqZero() {
System.out.println("\n**** aEqAnyAndbEqZero ****");
// 2. If a is any value except NaN and b = 0 then the result is 1.0.
System.out.println(Math.pow(2, 0));
assertTrue(Math.pow(2, 0) == 1);
}
@Test
public void aEqNegativeInfinityAndbGtZero() {
System.out.println("\n**** aEqNegativeInfinityAndbGtZero ****");
// 3. If a = NegativeInfinity and b is < 0 then the result is 0.0.
System.out.println(Math.pow(Double.NEGATIVE_INFINITY, -1));
assertTrue(Math.pow(Double.NEGATIVE_INFINITY, -1) == 0);
}
@Test
public void aEqNegativeInfinityAndbIsPostiveOddInt() {
System.out.println("\n**** aEqNegativeInfinityAndbIsPostiveOddInt ****");
// 4. If a = NegativeInfinity and b is a + odd integer then the result is
// NegativeInfinity.
System.out.println(Math.pow(Double.NEGATIVE_INFINITY, 1));
assertTrue(Math.pow(Double.NEGATIVE_INFINITY, 1) == Double.NEGATIVE_INFINITY);
}
@Test
public void aEqNegativeInfinityAndbIsNotPostiveOddInt() {
System.out.println("\n**** aEqNegativeInfinityAndbIsNotPostiveOddInt ****");
// 5. If a = NegativeInfinity and b is not a + odd integer then the result is PositiveInfinity.
System.out.println(Math.pow(Double.NEGATIVE_INFINITY, 2));
assertTrue(Math.pow(Double.NEGATIVE_INFINITY, 2) == Double.POSITIVE_INFINITY);
// 5. If a = NegativeInfinity and b is not a + odd integer, then the result is PositiveInfinity.
System.out.println(Math.pow(Double.NEGATIVE_INFINITY, 1.5));
assertTrue(Math.pow(Double.NEGATIVE_INFINITY, 1.5) == Double.POSITIVE_INFINITY);
}
@Test
public void aLtZeroAndbNotInteger() {
System.out.println("\n**** aLtZeroAndbNotInteger ****");
// 6. If a -1 but -1 but < 1 and b = PositiveInfinity then the result is 0.
System.out.println(Math.pow(-0.5, Double.POSITIVE_INFINITY));
assertTrue(Math.pow(-0.5, Double.POSITIVE_INFINITY) == 0);
}
@Test
public void aLtNegative1OrGtPositive1AndbEqNegativeInfinity() {
System.out.println("\n**** aLtNegative1OrGtPositive1AndbEqNegativeInfinity ****");
// 10. If a 1 and b equals NegativeInfinity, then the result is 0.
System.out.println(Math.pow(1.5, Double.NEGATIVE_INFINITY));
assertTrue(Math.pow(1.5, Double.NEGATIVE_INFINITY) == 0);
}
@Test
public void aLtNegative1OrGtPositive1AndbEqPositiveInfinity() {
System.out.println("\n**** aLtNegative1OrGtPositive1AndbEqPositiveInfinity ****");
// 11. If a 1 and b = PositiveInfinity then the result is PositiveInfinity.
System.out.println(Math.pow(1.5, Double.POSITIVE_INFINITY));
assertTrue(Math.pow(1.5, Double.POSITIVE_INFINITY) == Double.POSITIVE_INFINITY);
}
@Test
public void aEqZeroAndbLtZero() {
System.out.println("\n**** aEqZeroAndbLtZero ****");
// 12. If a = 0 and b 0 the result is 0.
System.out.println(Math.pow(0, 1));
assertTrue(Math.pow(0, 1) == 0);
}
@Test
public void aEqOneAndbAny() {
System.out.println("\n**** aEqOneAndbAny ****");
// 14. If a = 1 and b is any value except NaN the result is 1.
System.out.println(Math.pow(1, 500));
assertTrue(Math.pow(1, 500) == 1);
}
@Test
public void aEqPositiveInfinityAndbLtZero() {
System.out.println("\n**** aEqPositiveInfinityAndbLtZero ****");
// 15. If a = PositiveInfinity and b is 0 the result is PositiveInfinity.
System.out.println(Math.pow(Double.POSITIVE_INFINITY, 1));
assertTrue(Math.pow(Double.POSITIVE_INFINITY, 1) == Double.POSITIVE_INFINITY);
}
}
The methods demonstrate the rules covered in the table above.
- aOrbEqNaN validates
case 1. - aEqAnyAndbEqZero validates
case 2. - aEqNegativeInfinityAndbGtZero
validates case 3. - aEqNegativeInfinityAndbIsPostiveOddInt
validates case 4. - aEqNegativeInfinityAndbIsNotPostiveOddInt
validates case 5. - aLtZeroAndbNotInteger
validates case 6. - aEqNegative1AndbEqNegativeInfinityOrPositiveInfinity
validates case 7. - aGtNegative1ButLtPosive1AndbEqNegativeInfinity
validates case 8. - aGtNegative1ButLtPositve1AndbEqPositiveInfinity
validates case 9. - aLtNegative1OrGtPositive1AndbEqNegativeInfinity
validates case 10. - aLtNegative1OrGtPositive1AndbEqPositiveInfinity
validates case 11. - aEqZeroAndbLtZero validates
case 12. - aEqZeroAndbGtZero validates
case 13. - aEqOneAndbAny validates
case 14. - aEqPositiveInfinityAndbLtZero
validates case 15. - aEqPositiveInfinityAndbGtZero
validates case 16.
Right-click the test class and select Run As > JUnit Test. The result is shown below.
You will also see the following output in the console.
JUnit Test Output
**** aLtZeroAndbNotInteger **** NaN **** aEqZeroAndbGtZero **** 0.0 **** aEqNegativeInfinityAndbIsPostiveOddInt **** -Infinity **** aEqZeroAndbLtZero **** Infinity **** aEqPosInfinityAndbGtZero **** Infinity **** aEqAnyAndbEqZero **** 1.0 **** aEqPositiveInfinityAndbLtZero **** 0.0 **** aGtNegative1ButLtPosive1AndbEqNegativeInfinity **** Infinity **** aEqNegative1AndbEqNegativeInfinityOrPositiveInfinity **** NaN NaN **** aLtNegative1OrGtPositive1AndbEqNegativeInfinity **** 0.0 0.0 **** aGtNegative1ButLtPositve1AndbEqPositiveInfinity **** 0.0 **** aEqNegativeInfinityAndbIsNotPostiveOddInt **** Infinity Infinity **** aLtNegative1OrGtPositive1AndbEqPositiveInfinity **** Infinity Infinity **** aEqNegativeInfinityAndbGtZero **** -0.0 **** aEqOneAndbAny **** 1.0 **** aOrbEqNaN **** NaN NaN
3. Math.pow Java Example – Summary
In this example, we examined and tested the Math::pow static method of the Math class, an essential class included in the java.lang package.
4. Download the Source Code
This was a Math.pow Java Example.
You can download the full source code of this example here: Math.pow Java Example


