Double Trees
1. What is a double tree?
In the word “double tree” we will have to define first what is double and then what is a tree to get the full meaning. In English double means two or binary. Next, when we see the word tree, we can think of a big plant with repetitive branches, leaves, and fruits. From this vague definition, we can deduce a technical one as such: A double tree is a repetitive tree data structure that has at most 2 children nodes. Double trees have a few characteristics that make them easily identifiable which are:
- The total nodes or branches originating from the main branch are two.
- The number of
nodesor branches at the lowest level are equal to all the number of nodes before the lowest level plus 1.
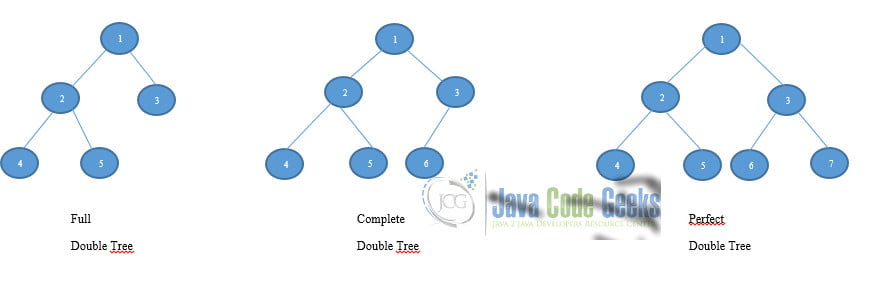
Each data element stored in a tree structure is called a node in Java. A tree node consists of 3 parts which are: data, a pointer to the left child, and a pointer to the right child. In Java, we can represent a tree node using a class. Similarly, there are 3 types of double trees based on their structure namely: Complete, full, and perfect double trees. An illustration is as shown:
In this article, we will focus on a perfect double tree.
2. Converting Trees to Double Trees
The conversion of trees to double trees is done in a one-to-one mapping. That is the reason why generally, a double tree is still a tree. The conversion of trees to double trees can be done in two steps as such:
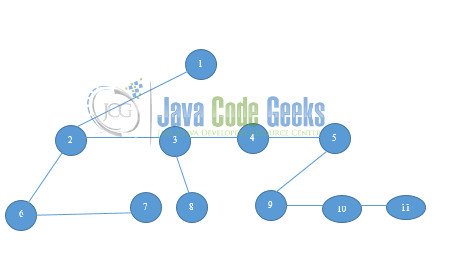
- Delete all the branches originating in every
nodeexcept the extreme left branch. - Trace the edges of the nodes to form a path toward the right.
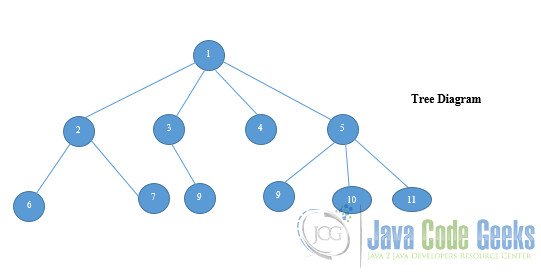
Once this is done, we are to choose the left and right sons for each node. The left is the node that is immediately below the root node and the right son is the node to the opposite of the left son that forms a horizontal line with its predecessor. Let’s take an example, assuming we have a tree as shown in the figure below and we need to convert it into a double tree we will have to follow the steps listed above in order to obtain the results as such:
Following step 1 instructions, the diagram will change to the following:
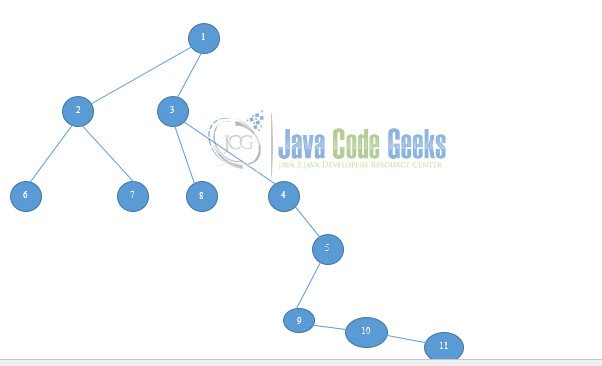
Following step 2 instructions, the diagram above will change to this:
3. Double Trees Java Implementation
In order to implement a double tree in Java, there are certain prerequisites we need to know which are:
- We are to start with the
root nodesas shown:
Node<String> root = new Node<>("root");Once we have our root, we can add the first child node using addChild which adds a child node and assigns it to a parent node. This process is referred as insertion otherwise deletion(removing nodes).
Node<String> node1 = root.addChild
(new Node<String>("node 1"));We have to continue adding nodes using that same process until we have a complex hierarchical structure. In order to implement a double tree, we will use a development environment like Intellij for illustrative purposes. Now let’s see how to implement the logic as such:
- Open IntelliJ and create a new project with the name Double Tree.
- Implement the code as shown below and run it
package org.example.doubletree;
import java.util.LinkedList;
public class DoubleTree {
public static void main(String[] args) {
DoubleTree.Node root = new DoubleTree.Node(2);
DoubleTree.Node temp = null;
temp = new DoubleTree.Node(4);
root.left = temp;
temp = new DoubleTree.Node(6);
root.right = temp;
temp = new DoubleTree.Node(8);
root.left.left = temp;
temp = new DoubleTree.Node(10);
root.left.right = temp;
temp = new DoubleTree.Node(12);
root.right.left = temp;
temp = new DoubleTree.Node(14);
root.right.right = temp;
temp = new DoubleTree.Node(16);
root.left.left.left = temp;
temp = new DoubleTree.Node(18);
root.left.left.right = temp;
temp = new DoubleTree.Node(20);
root.left.right.left = temp;
temp = new DoubleTree.Node(22);
root.left.right.right = temp;
temp = new DoubleTree.Node(24);
root.right.left.left = temp;
temp = new DoubleTree.Node(26);
root.right.left.right = temp;
temp = new DoubleTree.Node(28);
root.right.right.left = temp;
temp = new DoubleTree.Node(30);
root.right.right.right = temp;
printBinaryTree(root);
}
public static class Node {
public Node(int data) {
this.data = data;
}
int data;
Node left;
Node right;
}
public static void printBinaryTree(Node root) {
LinkedList<Node> treeLevel1 = new LinkedList<Node>();
treeLevel1.add(root);
LinkedList<Node> temp = new LinkedList<Node>();
int counter = 0;
int height = heightOfTree(root) - 1;
//System.out.println(height);
double numberOfElements = (Math.pow(2,(height + 1)) - 1) ;
//System.out.println(numberOfElements);
while (counter <= height) {
Node removed = treeLevel1.removeFirst();
if (temp.isEmpty()) {
printSpace(numberOfElements / Math.pow(2, counter + 1), removed);
} else {
printSpace(numberOfElements / Math.pow(2, counter), removed);
}
if (removed == null) {
temp.add(null);
temp.add(null);
} else {
temp.add(removed.left);
temp.add(removed.right);
}
if (treeLevel1.isEmpty()) {
System.out.println("");
System.out.println("");
treeLevel1 = temp;
temp = new LinkedList<>();
counter++;
}
}
}
public static void printSpace(double n, Node removed) {
for (; n > 0; n--) {
System.out.print("\t");
}
if (removed == null) {
System.out.print(" ");
}
else {
System.out.print(removed.data);
}
}
public static int heightOfTree(Node root) {
if (root == null) {
return 0;
}
return 1 +
Math.max(heightOfTree(root.left),
heightOfTree(root.right));
}
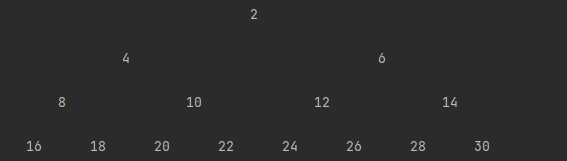
}The output of our program is as such:
In this example, we used the level order transversal which consists of transversing based on the level of the tree moving from the nodes corresponding to level 0 and then level 1 and so on. In the example above, the level order will be: (root) 2->4->6->8->10->12->14->16->18->20->22->24->26->28->30. There are other traversals such as in-order, pre-order, and post-order which you can use the idea behind in order to try and implement one. This brings us to the end of double trees in this article, thanks for your kind attention.
You can download the full source code of this example here: Double Trees