Dijkstra’s Algorithm Java Example
In this article, we will show a Dijkstra’s Algorithm Example in Java. First of all, we talk about what is the Dijkstra’s Algorithm and why we use it and then we analyze the algorithm with some examples.
1. Introduction
The Dijkstra’s Algorithm is an algorithm that is used to find the shortest path between two cities on a map or otherwise in programming the shortest path between two nodes in a graph. This algorithm works on graphs that don’t have negative weights on the edges so otherwise, it will not print the correct result. On these occasions, you can use other algorithms such us Bellman-Ford or Floyd-Warshall. We can see the use of the Dijkstra’s algorithm at the OSPF protocol which is the internal network gateway protocol of the Internet.
2. Technologies Used
The example code in this article was built and run using:
- Java 1.8.231(1.8.x will do fine)
- Eclipse IDE for Enterprise Java Developers-Photon
3. Step-by-step example of the Dijkstra’s Algorithm in Java
In this section, we analyze the Dijkstra’s Algorithm step by step. Here we use this graph as an example to help you understand better this algorithm.
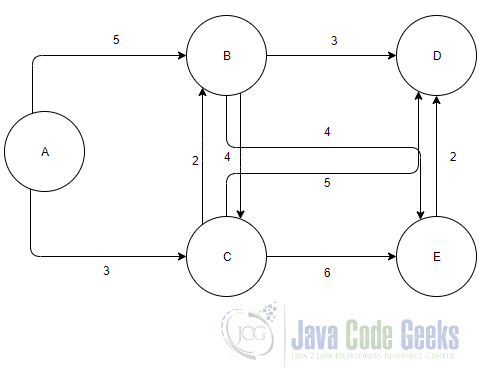
As we know Dijkstra’s algorithm is greedy. This means that we take the shorter path to go from one node to the other. The algorithm is complete when we visit all the nodes of the graph. Be careful though, sometimes when we find a new node there can be shorter paths through it from a visited node to another already visited node. We can see below the steps to complete the Dijkstra’s algorithm.
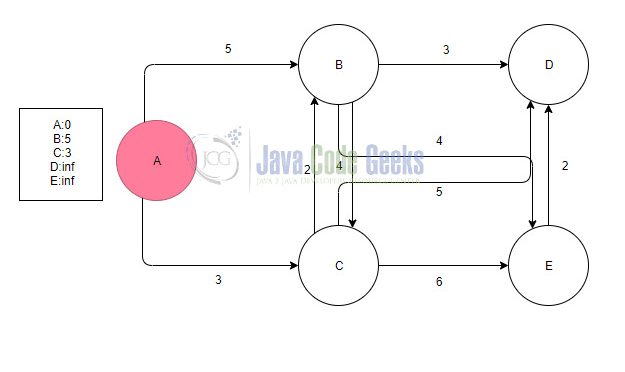
We can start with node A and we have 2 roads. The first is from A to B with 5 weight and to A to C with 3 weight. So we can write in our list with visited nodes the 2 new nodes(B, C ) and the weights to get there. Then as we said before we choose the A -> C path.
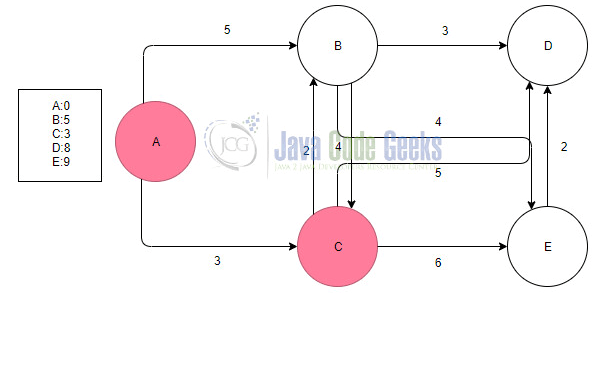
When we visit C node we can see that we have 3 paths. The first path is C to B, the second is C to D and the C to E. So we write to our list the two new nodes and we choose the shortest path which is C to B. A useful detail is that A -> B and A -> B -> C paths have the same weight in a different situation we must select the shortest path.
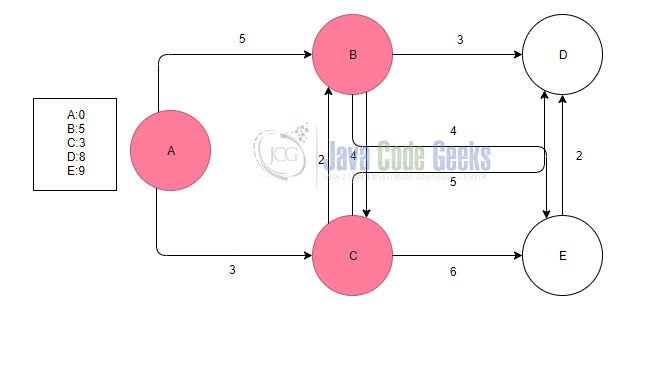
Now at B, we have 3 paths B to D, B to E and B back to C. We choose the shortest path which is B to D and we write in our list the new weights of the paths from A to other nodes if there are any existing.
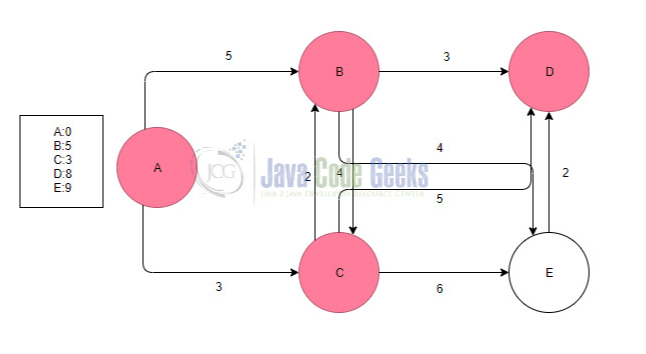
Now as we can see there aren’t new paths from D which connects it to E. In that case, we return to the previous node check the shortest path. Now there is a path with 4 weight which goes to E and a path which goes to C. In this case, we choose any path we like. In the end, we can see that whatever option we take the path from A to E has the same weight because the shortest paths are written on the list. Finally, we can see all the paths that we used.
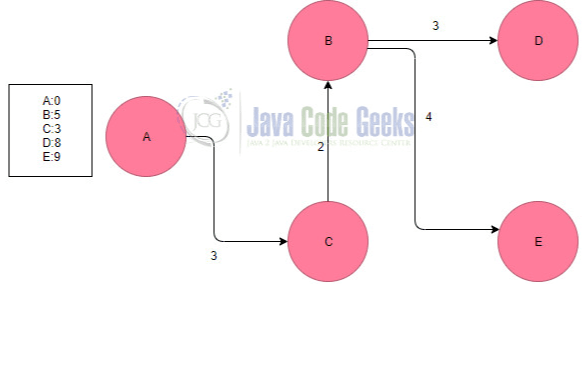
4. Code implementation of the Dijkstra’s Algorithm in Java
In this section, we create an example code in which we can see the Dijkstra’s algorithm.
First of all we must create the Edges and Vertices of the graph so :
Vert.java
import java.util.ArrayList;
import java.util.List;
public class Vert implements Comparable {
private boolean visited;
private String name;
private List List;
private double dist = Double.MAX_VALUE;
private Vert pr;
public Vert(String name) {
this.name = name;
this.List = new ArrayList();
}
public List getList() {
return List;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public void setList(List List) {
this.List = List;
}
public void addNeighbour(Edge edge) {
this.List.add(edge);
}
public boolean Visited() {
return visited;
}
public void setVisited(boolean visited) {
this.visited = visited;
}
public Vert getPr() {
return pr;
}
public void setPr(Vert pr) {
this.pr = pr;
}
public double getDist() {
return dist;
}
public void setDist(double dist) {
this.dist = dist;
}
@Override
public String toString() {
return this.name;
}
@Override
public int compareTo(Vert otherV) {
return Double.compare(this.dist, otherV.getDist());
}
}
Edge.java
public class Edge {
private double weight;
private Vert startVert;
private Vert targetVert;
public Edge(double weight, Vert startVert, Vert targetVert) {
this.weight = weight;
this.startVert = startVert;
this.targetVert = targetVert;
}
public double getWeight() {
return weight;
}
public void setWeight(double weight) {
this.weight = weight;
}
public Vert getStartVert() {
return startVert;
}
public void setStartVert(Vert startVert) {
this.startVert = startVert;
}
public Vert getTargetVert() {
return targetVert;
}
public void setTargetVert(Vert targetVert) {
this.targetVert = targetVert;
}
} In these two codes, we create the basic graph that is the edges, vertices, weights and some methods to help us understand the edges that were visited.
Below we create a class that help us find the shortest path of the graph:
PathFinder.java
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.PriorityQueue;
public class PathFinder {
public void ShortestP(Vert sourceV){
sourceV.setDist(0);
PriorityQueue priorityQueue = new PriorityQueue();
priorityQueue.add(sourceV);
sourceV.setVisited(true);
while( !priorityQueue.isEmpty() ){
Vert actualVertex = priorityQueue.poll();
for(Edge edge : actualVertex.getList()){
Vert v = edge.getTargetVert();
if(!v.Visited())
{
double newDistance = actualVertex.getDist() + edge.getWeight();
if( newDistance < v.getDist() ){
priorityQueue.remove(v);
v.setDist(newDistance);
v.setPr(actualVertex);
priorityQueue.add(v);
}
}
}
actualVertex.setVisited(true);
}
}
public List getShortestPathTo(Vert targetVertex){
List path = new ArrayList();
for(Vert vertex=targetVertex;vertex!=null;vertex=vertex.getPr()){
path.add(vertex);
}
Collections.reverse(path);
return path;
}
}
Finally, we create a main that we give the edges and the vertices of the graph and the code give as the results:
PathFinder.java
public class Dijkstra {
public static void main(String[] args) {
Vert vA = new Vert("A");
Vert vB = new Vert("B");
Vert vC = new Vert("C");
Vert vD = new Vert("D");
Vert vE = new Vert("E");
vA.addNeighbour(new Edge(3,vA,vC));
vA.addNeighbour(new Edge(5,vA,vB));
vC.addNeighbour(new Edge(2,vC,vB));
vC.addNeighbour(new Edge(6,vC,vE));
vC.addNeighbour(new Edge(5,vC,vD));
vB.addNeighbour(new Edge(4,vB,vC));
vB.addNeighbour(new Edge(3,vB,vD));
vB.addNeighbour(new Edge(4,vB,vE));
vE.addNeighbour(new Edge(2,vE,vD));
PathFinder shortestPath = new PathFinder();
shortestPath.ShortestP(vA);
System.out.println("Minimum distance from A to B: "+vB.getDist());
System.out.println("Minimum distance from A to C: "+vC.getDist());
System.out.println("Minimum distance from A to D: "+vD.getDist());
System.out.println("Minimum distance from A to E: "+vE.getDist());
System.out.println();
System.out.println("Shortest Path from A to B: "+shortestPath.getShortestP(vB));
System.out.println("Shortest Path from A to C: "+shortestPath.getShortestP(vC));
System.out.println("Shortest Path from A to D: "+shortestPath.getShortestP(vD));
System.out.println("Shortest Path from A to E: "+shortestPath.getShortestP(vE));
}
}
5. Download the Source Code
You can download the full source code of this example here: Dijkstra’s Algorithm Java Example


