Bucket Sort Algorithm

1. Introduction

In this article, we will look specifically at the Bucket Sort Algorithm, which is a type of Sorting Algorithm. An Algorithm in general can be thought of as a set of instructions that can be executed sequentially to resolve a problem or achieve a specific outcome. Algorithms are usually used to resolve problems of different kinds in either Mathematical or Computing professions.

In Computing, Algorithms can be categorized into different types based on their similarity and functionality in solving a problem. The following are examples of types of Algorithms in Computer Science:

• Searching Algorithms
• Sorting Algorithms
• Hashing Algorithms
• Recursive Algorithms
• Dynamic Programming Algorithms
• Brute Force Algorithms
• Randomized Algorithms and
• Greedy Algorithms.

Here will focus on one of the Sorting Algorithm types, the Bucket Sort Algorithm.

2. Technologies to be used for this bucket sort example:

1. Operating System: Ubuntu 20.04 or Windows 10.
2. IDE: (IntelliJ IDEA Community Edition 2022.2 on Ubuntu) or (IntelliJ IDEA2021.3.3 Community Edition on Windows 10).
3. (Java OpenJDK version 11.0.16 on Ubuntu) and (Java JDK 1.8.0_341 on Windows).

3. Bucket Sort Algorithm

The Bucket Sort Algorithm works by dividing an unsorted array of elements into smaller groups of elements or lists called buckets. Each of these buckets is then sorted individually and then afterward, all sorted buckets are merged into one sorted array.

The Bucket Sort Algorithm uses a Scatter Gather Approach, which is the mechanism used to break the main unsorted array down into smaller buckets (arrays or lists), sort the individual buckets, and merge the sorted buckets into a completely sorted array.

4. The Scatter-Gather Approach

The Bucket Sort Algorithm implements the following steps:

1. Create an empty bucket list (or appropriate data structure) List<ArrayList<>>.
2. Initialize it to a size of N + 1, where N is the number of elements in the array.
3. Find the maximum value M in the unsortedArray[ ].
4. As you traverse the unsorted array unsortedArray[ ], insert each array element of unsortedArray[ i ] into the buckets list by calculating the bucket index as follows: bucketIndex = [floor(N * array[ i ] / M)]
5. If the elements of the array are of type float, we calculate the bucket index using the following formula [N * unsortedArray[ i ]].
6. Sort each bucket using an appropriate sorting algorithm or sort it recursively, using bucket sort.
7. Merge the sorted buckets into a sorted array.

This is illustrated with the following visual example:

int[ ] unsortedArray = {12, 27, 4, 15, 28, 9, 21, 1, 19, 6};

In this demonstration of the bucket sort algorithm, we will use a List of ArrayLists as the data structure for the bucket list.

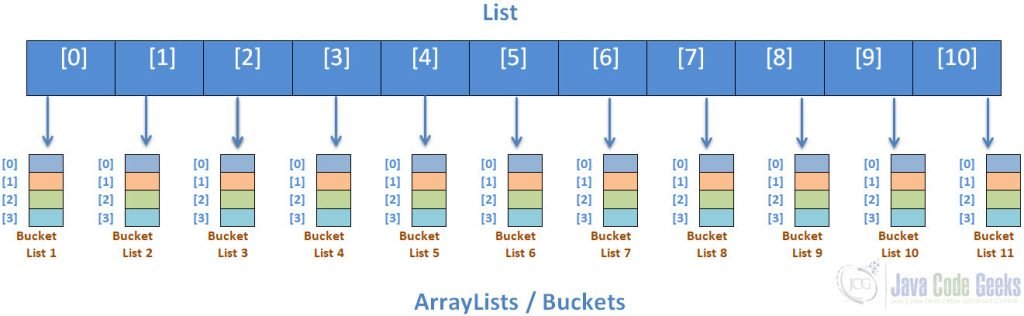
The Scatter Approach

Here the elements of the unsorted array unsortedArray[ ] are split into separate buckets, and the Indexes of each bucket into which they will be placed are calculated as follows:

The elements are then split as follows:

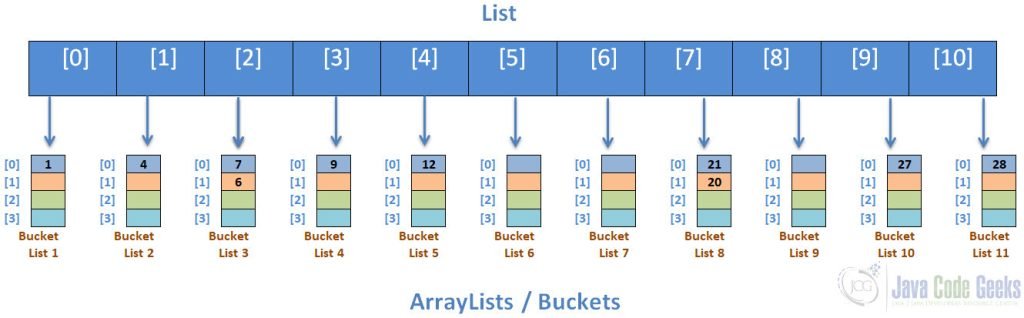
The buckets are then sorted using any sorting algorithms:

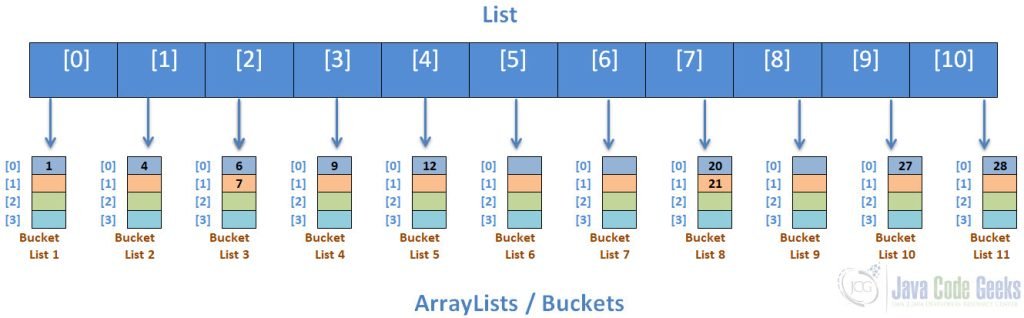
The Gather Approach

The Gather Approach involves merging the sorted buckets into a sorted array as follows:

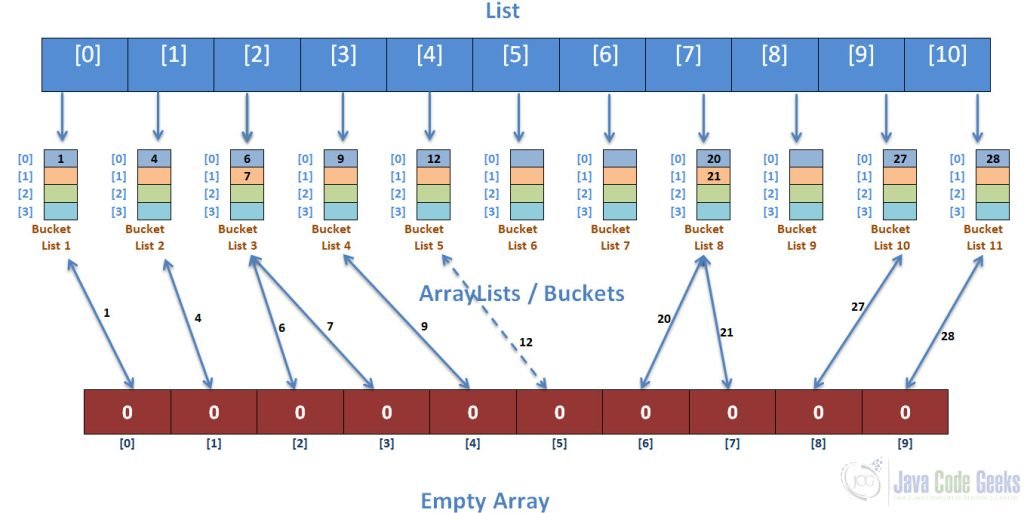
Finally the sorted ArrayList values are copied to an array which is shown below:

5. Bucket Sort Implementation

The following is a Java implementation of the Bucket Sort Algorithm:

Bucket Sort Java Code

package com.javacodegeeks.bucketsort;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class BucketSort {

    //A getMaxValue function to determine the maximum value in an array.
    public static int getMaxValue(int[] m){
        int maxValue = 0;
        for(int i = 0; i  maxValue){
                maxValue = m[i];
            }
        }
        return maxValue;
    }

    //A printOutPut method to display the contents of the sorted array.
    public static void printOutput(int[] sortedArray){
        System.out.println(" The sorted array is as follows:");
        for(int i = 0; i < sortedArray.length; i++){
            System.out.print(sortedArray[i] + " ");
        }
    }

    //This implementation of the Bucket Sort Algorithm uses a List of ArrayLists as the bucket data structure.
    public static int[] bucketSortAlgorithm(int[] unsortedArray){

        int n = unsortedArray.length;
        int maxElement = getMaxValue(unsortedArray);
        int bucketListSize = n + 1;

        //Create the bucket list and initialize it to the size of the unsortedArray's length + 1.
        List<ArrayList> buckets = new ArrayList(bucketListSize);

        //Create empty buckets
        for(int i = 0; i < bucketListSize; i++) {
            buckets.add(new ArrayList());
        }

        /*Traverse the unsortedArray and arrange the elements into buckets.
          This is the Scatter part in the Scatter Gather Approach.*/
        int bucketIndex = 0;
        for(int i = 0; i < n; i++){
            bucketIndex = (int)(Math.floor((unsortedArray[i] * n)/maxElement));

            buckets.get(bucketIndex).add(unsortedArray[i]);
            System.out.println("The added elements are: ");
            System.out.println(buckets);
        }

        /*Sort each bucket using an appropriate sorting algorithm or recursively use
        the Bucket Sort Algorithm*/
        for(int i = 0; i < bucketListSize; i++){
            Collections.sort(buckets.get(i));
            System.out.println("The sorted buckets are as follows:" + buckets);
        }

        /*Merge the sorted buckets into a single sorted array
        This is known as the Gather part in the Scatter Gather Approach*/
        int arrayIndex = 0;
        List sortedArrayList = new ArrayList();
        for(int i = 0; i < bucketListSize; i++){
            int bucketSize = buckets.get(i).size();
            for (int j = 0; j < bucketSize; j++) {
                List intValue = buckets.get(j);
                sortedArrayList.add(buckets.get(i).get(j));
            }
        }
        //Copy the contents of the sorted List into an empty array.
        int[] sorted_arr = sortedArrayList.stream().mapToInt(Integer::intValue).toArray();

        return sorted_arr;
    }

    public static void main(String[] args) {

        int[] array = {12, 27, 4, 7, 28, 9, 21, 1, 20, 6};
        /*The following arrays can be uncommented and tested to see how the Algorithm works with different values*/
        //int[] array = {67, 23, 2, 80, 44, 90, 33, 56, 73, 7, 25, 14, 48, 69, 84, 78, 36, 52, 18, 62};
        //int[] array = {94, 87, 3, 77, 16, 35, 67, 5};

        //Display of the unsorted Array before sorting.
        System.out.println("The unsorted array is as follows:" );
        for(int i = 0; i < array.length; i++){
            System.out.print(array[i] + " ");
        }

        //A BucketSort object is created.
        BucketSort b = new BucketSort();

        //The BucketSort object is used to make a call to the bucketSort Algorithm and the output is displayed.
        printOutput(b.bucketSortAlgorithm(array));
    }
}

Output:

To run this example in IntelliJ IDEA, create a new project and create a class named BucketSort.java. Copy the above code into the created file. Build the project and Run BucketSort.java

Alternatively, you can download the source code of this example below and run it in the IDE of your choice.

5. Complexity of Algorithms

The amount of time, storage, or other resources needed to execute an Algorithm is known as the computational Complexity of an Algorithm.

It can be determined in either one of two ways:

• Its Time Complexity or
• Its Space Complexity.

The Time Complexity of an Algorithm determines how it performs in terms of processing speed as its input size increases. This is basically called the running time of an algorithm and it’s estimated by counting the number of operations performed by the Algorithm when used with very large data sets.

The Space Complexity of an Algorithm takes into consideration how much memory the Algorithm uses whilst executing its instructions or steps.

In general, Algorithms perform at different rates based on the inputs or data sets they operate on. The performance of an algorithm for small inputs may not be significant, but as the input size increases, that is when its performance is tested.

For the Bucket Sort Algorithm to perform at its best, the number of buckets created should be equal to the number of elements in the array or data structure used. This will ensure that the elements are distributed over several buckets and its Time Complexity would be O(N). This is known as its Best Case Time Complexity.

If the number of buckets for the Algorithm is poorly chosen, for example choosing to use just one bucket, then this would affect the performance of the Algorithm greatly. Such a case would be considered its Worst Case scenario and its Time Complexity would be O(N²).

The overall performance of the Algorithm is determined by the algorithm used to sort each bucket individually. As a result, the worst-case scenario would range from O(N²) to O(NLogN).

6. Conclusion

Practical applications of the Bucket Sort Algorithm according to airfocus.com include:

1. Speed up the sorting process of data sets and
2. Organize and assign prioritization lists based on the time they may take.

7. Download the source code

This was an example of the BucketSort Algorithm.

Do you want to know how to develop your skillset to become a Java Rockstar?

Subscribe to our newsletter to start Rocking right now!

To get you started we give you our best selling eBooks for FREE!

1. JPA Mini Book

2. JVM Troubleshooting Guide

3. JUnit Tutorial for Unit Testing

4. Java Annotations Tutorial

5. Java Interview Questions

6. Spring Interview Questions

7. Android UI Design

and many more ....

I agree to the Terms and Privacy Policy

Sign up

Thank you!

We will contact you soon.