Breadth First Search Java Example

1. Introduction

Breadth First Search (BFS algorithm) is a traversing or searching algorithm for a tree or graph data structure. BFS starts at the tree root, and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.

A tree is a nonlinear data structure which includes a root and sub-trees of children. A Binary Tree is the most commonly used tree in which every node can have at most two children.

A graph is a nonlinear data structure which includes a set of vertices and a set of edges. An edge is a pair of vertices that are connected. A tree can be considered as a graph with no loops.

In this example, I will demonstrate how to:

• Traverse a Binary Tree via BFS and Depth First Search (DFS)
• Traverse a general Tree via BFS
• Traverse a graph via BFS
• Search an item in a Binary Tree via BFS and DFS
• Search an item in a general Tree via BFS
• Search an item in a graph via BFS

2. Technologies Used

The example code in this article was built and run using:

• Java 11
• Maven 3.3.9
• Junit 4.12
• Jfreechart 1.5.0
• Eclipse Oxygen

3. Maven Project

In this step, I will create a Maven project which includes several classes to demonstrate the BFS. I will use Jfreechart to show the time complexity in a line graph for traversing a Binary Tree with both BFS algorithm and DFS.

3.1 Dependencies

I will include Junit and Jfreechart in the pom.xml.

pom.xml

<project xmlns="http://maven.apache.org/POM/4.0.0"
	xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
	xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
	<modelVersion>4.0.0</modelVersion>
	<groupId>org.jcg.zheng.demo</groupId>
	<artifactId>selection-sort</artifactId>
	<version>0.0.1-SNAPSHOT</version>

	<properties>
		<project.build.sourceEncoding>UTF-8</project.build.sourceEncoding>
	</properties>

	<build>
		<sourceDirectory>src</sourceDirectory>
		<plugins>
			<plugin>
				<artifactId>maven-compiler-plugin</artifactId>
				<version>3.8.0</version>
				<configuration>
					<release>11</release>
				</configuration>
			</plugin>
		</plugins>
	</build>
	<dependencies>
		<dependency>
			<groupId>junit</groupId>
			<artifactId>junit</artifactId>
			<version>4.12</version>
		</dependency>
		<dependency>
			<groupId>org.jfree</groupId>
			<artifactId>jfreechart</artifactId>
			<version>1.5.0</version>
		</dependency>
	</dependencies>
</project>

3.2 Constant Values

In this step, I will create a ConstantValuesclass which holds the constant values used in the project.

ConstantValues.java

package org.jcg.zheng;

public class ConstantValues {

 public static final String BREADTH_FIRST_SEARCH_CSV = "BreadthFirst_Search.csv";

 public static final String DEPTH_FIRST_SEARCH_CSV = "DepthFirst_Search.csv";

 public static final String BREADTH_FIRST_TRAVERAL_CSV = "BreadthFirst_Traverse.csv";

 public static final String DEPTH_FIRST_TRAVERSE_CSV = "DepthFirst_Traverse.csv";


}

3.3 Line Graph Chart

In this step, I will create a LineGraphChart class which extends from org.jfree.chart.ui.ApplicationFrame. It will draw a line graph for the execution time of BFS and DFS for a binary tree along with the input size N.

LineGraphChart.java

package org.jcg.zheng;

import java.awt.BorderLayout;
import java.awt.Color;
import java.io.File;
import java.io.IOException;
import java.nio.charset.Charset;
import java.nio.file.Files;
import java.util.HashMap;
import java.util.Map;

import javax.swing.JPanel;

import org.jfree.chart.ChartFactory;
import org.jfree.chart.ChartPanel;
import org.jfree.chart.JFreeChart;
import org.jfree.chart.axis.NumberAxis;
import org.jfree.chart.axis.ValueAxis;
import org.jfree.chart.plot.PlotOrientation;
import org.jfree.chart.plot.XYPlot;
import org.jfree.chart.renderer.xy.StandardXYItemRenderer;
import org.jfree.chart.ui.ApplicationFrame;
import org.jfree.data.xy.XYDataset;
import org.jfree.data.xy.XYSeries;
import org.jfree.data.xy.XYSeriesCollection;

public class LineGraphChart extends ApplicationFrame {

	private static final long serialVersionUID = 8024827403766653799L;

	public static void main(String[] args) {

		final LineGraphChart demo = new LineGraphChart("Big O");
		demo.pack();
		demo.setVisible(true);
	}

	private XYPlot plot;

	public LineGraphChart(String title) {
		super(title);

		final XYDataset dataset1 = createRandomDataset("BreadthFirst_Search",
				readCoordinates(ConstantValues.BREADTH_FIRST_SEARCH_CSV));
		final JFreeChart chart = ChartFactory.createXYLineChart("Big O Notations", "Input Size", "Value", dataset1,
				PlotOrientation.VERTICAL, true, true, false);
		chart.setBackgroundPaint(Color.white);

		this.plot = chart.getXYPlot();
		this.plot.setBackgroundPaint(Color.lightGray);
		this.plot.setDomainGridlinePaint(Color.white);
		this.plot.setRangeGridlinePaint(Color.white);
		final ValueAxis axis = this.plot.getDomainAxis();
		axis.setAutoRange(true);

		final NumberAxis rangeAxis2 = new NumberAxis("Range Axis 2");
		rangeAxis2.setAutoRangeIncludesZero(false);

		final JPanel content = new JPanel(new BorderLayout());

		final ChartPanel chartPanel = new ChartPanel(chart);
		content.add(chartPanel);

		chartPanel.setPreferredSize(new java.awt.Dimension(700, 500));
		setContentPane(content);

		this.plot.setDataset(1, createRandomDataset("BreadthFirst_Traveral",
				readCoordinates(ConstantValues.BREADTH_FIRST_TRAVERAL_CSV)));
		this.plot.setRenderer(1, new StandardXYItemRenderer());

		this.plot.setDataset(2,
				createRandomDataset("DepthFirst_Traveral", readCoordinates(ConstantValues.DEPTH_FIRST_TRAVERSE_CSV)));
		this.plot.setRenderer(2, new StandardXYItemRenderer());

		this.plot.setDataset(3,
				createRandomDataset("DepthFirst_Traveral", readCoordinates(ConstantValues.DEPTH_FIRST_SEARCH_CSV)));
		this.plot.setRenderer(3, new StandardXYItemRenderer());

	}

	private XYDataset createRandomDataset(final String label, Map<Long, Long> xyCoordinates) {
		XYSeriesCollection dataset = new XYSeriesCollection();
		XYSeries series = new XYSeries(label);

		xyCoordinates.forEach((k, v) -> {
			series.add(k, v);
		});

		dataset.addSeries(series);
		return dataset;
	}

	private Map<Long, Long> readCoordinates(String filename) {
		Map<Long, Long> xyCoordinates = new HashMap<>();
		try {
			File data = new File(filename);
			Files.readAllLines(data.toPath(), Charset.defaultCharset()).forEach(s -> {
				String[] values = s.split(",");
				xyCoordinates.put(Long.valueOf(values[0]), Long.valueOf(values[1]));
			});
		} catch (IOException e) {
			e.printStackTrace();
		}

		return xyCoordinates;
	}
}

3.4 Binary Tree Node

In this step, I will create a BinaryTreeNode class which has an integer value, left, and right BinaryTreeNode.

BinaryTreeNode.java

package org.jcg.zheng.data;

public class BinaryTreeNode {

	private int data;

	private BinaryTreeNode left;

	private BinaryTreeNode right;

	public BinaryTreeNode(int data) {
		this.data = data;
	}

	public int getData() {
		return data;
	}

	public BinaryTreeNode getLeft() {
		return left;
	}

	public BinaryTreeNode getRight() {
		return right;
	}

	public void setLeft(BinaryTreeNode left) {
		this.left = left;
	}

	public void setRight(BinaryTreeNode right) {
		this.right = right;
	}

	@Override
	public String toString() {
		return "BinaryTreeNode [data=" + data + ", left=" + left + ", right=" + right + "]";
	}

}

3.5 Tree Node

In this step, I will create a TreeNode generics class which has a generic data type and a list of children.

TreeNode.java

package org.jcg.zheng.data;

import java.util.ArrayList;
import java.util.List;

public class TreeNode<T> {
	public static <T> TreeNode<T> of(T data) {
		return new TreeNode<>(data);
	}

	private List<TreeNode<T>> children;

	private T data;

	private TreeNode(T data) {
		this.data = data;
		this.children = new ArrayList<>();
	}

	public TreeNode<T> addChild(T data) {
		TreeNode<T> child = new TreeNode<>(data);
		children.add(child);

		return child;
	}

	public List<TreeNode<T>> getChildren() {
		return children;
	}

	public T getData() {
		return data;
	}

}

3.6 Vertex

In this step, I will create a Vertex generic class which has a name for the vertex and set of connected Vertices. I also have a connect method to connect this object to the connectingVertex object.

Vertex.java

package org.jcg.zheng.data;

import java.util.HashSet;
import java.util.Set;

public class Vertex<T> {

	private Set<Vertex<T>> connectedVertices;

	private T name;

	public Vertex(T label) {
		super();
		this.name = label;
		this.connectedVertices = new HashSet<>();
	}

	public void connect(Vertex<T> connectingVertex) {
		if (this == connectingVertex) {
			throw new IllegalArgumentException("Cannot connect to iteself");
		}

		this.connectedVertices.add(connectingVertex);

		connectingVertex.connectedVertices.add(this);

	}

	public Set<Vertex<T>> getConnectedVertex() {
		return connectedVertices;
	}

	public T getName() {
		return name;
	}


	@Override
	public String toString() {
		return "Vertex [name=" + name + ", connectedVertex=" + connectedVertices + "]";
	}

}

3.7 Depth First Search

For a Tree data structure, DFS will start at the root node, and search all the children, including all possible branches for that node before backtracking. I will illustrate the traversing order with the following tree.

      10       
      /\
     9  12     
    /   /\
   4   11 16  

1 => 10, 9, 4
2 => 12, 11, 16

It starts from the root: 10. Then it moves to root’s left child: 9. Then it moves to 9’s child: 4. Then it backtracks to the root. Then it moves to its right child: 12. Then it moves to 12’s children: 11 and 16.

In this step, I will create a DepthFirst class to traverse a BinaryTreeNode. I will demonstrate the pre-order logic which traverses in node, left, and right order.

DepthFirst.java

package org.jcg.zheng.search;

import org.jcg.zheng.ConstantValues;
import org.jcg.zheng.data.BinaryTreeNode;

public class DepthFirst {

 public void traverse(BinaryTreeNode node) {
 if (node == null) {
 return;
 }

 System.out.print(node.getData() + " ");

 traverse(node.getLeft());
 traverse(node.getRight());
 }

 public BinaryTreeNode search(int value, BinaryTreeNode node) {

 BinaryTreeNode found = null;

 if (node == null) {
 return found;
 }

 if (node.getData() == value) {
 found = node;
 } else if (node.getData() > value) {
 found = search(value, node.getLeft());
 } else {
 found = search(value, node.getRight());
 }

 return found;
 }

}

As you can see, if the tree is deeply constructed, then it may encounter StackOverflow error.

3.8 Breadth First Search algorithm

For a Tree data structure, BFS will start at the root node, and search all the children, once all the children nodes have been searched, then move to next level nodes. This process is repeated for each level until reaching the end of tree or found the node.

I will illustrate with the traversing order with the following tree.

      10       --> 1 => 10
      /\
     9  12     --> 2 => 9, 12
    /   /\
   4   11 16   --> 3 => 4, 11, 16

It starts from the root: 10, and then moves to the 2nd level: 9 and 12, the 3rd level: 4, 11, and 16.

BFS on a tree utilizes a queue data structure. I create a queue and put the root node as the first element. Then it enters a while loop, as long as the queue is not empty, it polls the first element from the queue and adds its children to the queue. It finishes when the queue is empty.

BFS on a graph is very similar to the tree structure. The only difference is that a graph may have a loop or cycle. So it will check the already visited vertex to avoid the infinite loop.

I will illustrate the traversing order for a pentagon as the following:

    A   --> 1 => A
    /\
   B  E  --> 2 => B, E
   |  |
   C__D  --> 3 => C, D

It starts from vertex A and then checks B and E, finally visits C and D.

BFS can reduce the search time by stopping at any depth easily. This is a feature used in gaming software to find the items and enable the computer character to perform reasonable actions.

In this step, I will create a BreadthFirst class to traverse and search for BinaryTreeNode, TreeNode, and Vertex data classes.

BreadthFirst.java

package org.jcg.zheng.search;

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Set;

import org.jcg.zheng.ConstantValues;
import org.jcg.zheng.data.BinaryTreeNode;
import org.jcg.zheng.data.TreeNode;
import org.jcg.zheng.data.Vertex;

public class BreadthFirst<T> {

	public BinaryTreeNode search(int value, BinaryTreeNode node) {
		BinaryTreeNode found = null;
		Queue<BinaryTreeNode> q = new LinkedList<>();
		int visitedNodeCount = 0;
		q.add(node);

		while (!q.isEmpty()) {
			node = q.poll();
			visitedNodeCount++;

			if (node.getData() == value) {
				found = node;
				break;
			}

			if (node.getLeft() != null) {
				q.add(node.getLeft());
			}

			if (node.getRight() != null) {
				q.add(node.getRight());
			}
		}
		System.out.println("Visited " + visitedNodeCount + " nodes to find the key.");
		return found;
	}

	public TreeNode<T> search(T value, TreeNode<T> node) {
		TreeNode<T> found = null;
		Queue<TreeNode<T>> q = new LinkedList<>();

		q.add(node);

		while (!q.isEmpty()) {
			node = q.remove();
			System.out.println("Visited Node:" + node.getData());
			if (node.getData() != null && node.getData().equals(value)) {
				found = node;
				break;
			} else {
				q.addAll(node.getChildren());
			}
		}

		return found;
	}

	public Vertex<T> search(T value, Vertex<T> startVertex) {
		Set<Vertex<T>> alreadyVisited = new HashSet<>();
		Queue<Vertex<T>> q = new ArrayDeque<>();

		q.add(startVertex);

		Vertex<T> currentVertex;

		while (!q.isEmpty()) {
			currentVertex = q.remove();

			System.out.println("Visited Vertex:" + currentVertex.getName());
			if (currentVertex.getName() != null && currentVertex.getName().equals(value)) {
				return currentVertex;
			}

			alreadyVisited.add(currentVertex);
			q.addAll(currentVertex.getConnectedVertex());
			q.removeAll(alreadyVisited);
		}

		return null;

	}

	public List<Integer> traverse(BinaryTreeNode node) {
		List<Integer> treeNodes = new ArrayList<>();
		Queue<BinaryTreeNode> q = new LinkedList<>();

		q.add(node);

		while (!q.isEmpty()) {
			node = q.poll();
	
			treeNodes.add(node.getData());

			if (node.getLeft() != null) {
				q.add(node.getLeft());
			}

			if (node.getRight() != null) {
				q.add(node.getRight());
			}
		}
		
		return treeNodes;
	}

	public List<Integer> traverse(BinaryTreeNode node, int maxDepth) {
		List<Integer> treeNodes = new ArrayList<>();
		if (maxDepth < 0) {
			return treeNodes;
		}

		Queue<BinaryTreeNode> q = new LinkedList<>();
		q.add(node);

		int currentDepth = 0;

		while (!q.isEmpty()) {
			node = q.poll();
			treeNodes.add(node.getData());

			if (currentDepth++ > maxDepth)
				return treeNodes;
			

			if (node.getLeft() != null) {
				q.add(node.getLeft());
			}

			if (node.getRight() != null) {
				q.add(node.getRight());
			}
		}
		
		return treeNodes;
	}

	public void traverse(TreeNode<T> node) {
		Queue<TreeNode<T>> q = new LinkedList<>();

		q.add(node);

		while (!q.isEmpty()) {
			node = q.remove();

			System.out.print(node.getData() + "\t");
			q.addAll(node.getChildren());
		}
	}

	public void traverse(Vertex<T> startVertex) {

		Set<Vertex<T>> alreadyVisited = new HashSet<>();
		Queue<Vertex<T>> q = new ArrayDeque<>();

		q.add(startVertex);

		Vertex<T> currentVertex;

		while (!q.isEmpty()) {
			currentVertex = q.remove();
			System.out.print(currentVertex.getName() + "\t");

			alreadyVisited.add(currentVertex);
			q.addAll(currentVertex.getConnectedVertex());
			q.removeAll(alreadyVisited);
		}

	}
}

As you see here, I created 4 traverse methods: one for a graph, one for a generic tree, one for a binary tree, the last one for binary tree with the max depth. The one for graph use alreadyVisited variable to prevent the infinite loop.

4. JUnit Test

In this step, I will create a Junit test to traverse and search an element based on BFS for a BinaryTreeNode, TreeNode, and graph. I will compare the BFS with DFS on a BinaryTreeNode.

4.1 Test Binary Tree

In this step, I will create a TestBinaryTree class which has a tree root and add method. It’s used to build a binary tree with various sizes.

TestBinaryTree.java

package org.jcg.zheng.search;

import org.jcg.zheng.data.BinaryTreeNode;

public class TestBinaryTree {

	private BinaryTreeNode root;

	private BinaryTreeNode add(BinaryTreeNode current, int addingValue) {
		if (current == null) {
			return new BinaryTreeNode(addingValue);
		}

		if (addingValue < current.getData()) {
			current.setLeft(add(current.getLeft(), addingValue));
		} else if (addingValue == current.getData()) {
			return current;
		} else {
			current.setRight(add(current.getRight(), addingValue));
		}

		return current;
	}

	public void add(int value) {
		root = add(root, value);
	}

	public BinaryTreeNode getRoot() {
		return root;
	}

	public void setRoot(BinaryTreeNode root) {
		this.root = root;
	}
}

4.2 Binary Tree Traverse and Search Test

In this step, I will create a BinaryTreeSearchTraverseTest class which traverses and searches a BinaryTreeNode object via both BFS and DFS. All four tests use the same binary tree as the following:

         10
         / \
        1  11
        \   \
         2   12
         \    \
          3    13
           \    \
            4   14
            \     \
             5    15
             \      \
              6     16
               \      \
                7      17
                \       
                 8      
                 \   
                  9    
    

BinaryTreeSearchTraverseTest.java

package org.jcg.zheng.search;

import static org.junit.Assert.assertEquals;
import static org.junit.Assert.assertNotNull;
import static org.junit.Assert.assertNull;

import java.util.List;

import org.jcg.zheng.data.BinaryTreeNode;
import org.junit.After;
import org.junit.Before;
import org.junit.Rule;
import org.junit.Test;
import org.junit.rules.TestName;

public class BinaryTreeSearchTraverseTest {

	private DepthFirst dfTest = new DepthFirst();
	private BreadthFirst<String> bfTest = new BreadthFirst<>();

	protected BinaryTreeNode numberRoot;
	private TestBinaryTree testRoot = new TestBinaryTree();

	@Rule
	public TestName name = new TestName();

	public BinaryTreeSearchTraverseTest() {
		super();
	}

	@Before
	public void setup() {
		System.out.println( name.getMethodName() + " started.");

		testRoot.add(10);
		for (int i = 1; i < 17; i++) {
			testRoot.add(i);
		}

		numberRoot = testRoot.getRoot();
	}

	@After
	public void cleanup() {
		System.out.println("\n" + name.getMethodName() + " completed.\n");
	}

	@Test
	public void df_traverse() {
		dfTest.traverse(numberRoot);
	}

	@Test
	public void df_search() {
		BinaryTreeNode found = dfTest.search(3, numberRoot);
		assertNotNull(found);
		assertEquals(3, found.getData());
	}

	@Test
	public void bf_traverse() {
		List<Integer> nodes =  bfTest.traverse(numberRoot);
		
		assertEquals(16, nodes.size());
		assertEquals(10, nodes.get(0).intValue());
		assertEquals(1, nodes.get(1).intValue());
		assertEquals(11, nodes.get(2).intValue());
		assertEquals(2, nodes.get(3).intValue());
		assertEquals(12, nodes.get(4).intValue());
		
		System.out.println(nodes);
	}

	@Test
	public void bf_traverse_limit3() {
		List<Integer> nodesIn3Level = bfTest.traverse(numberRoot, 3);
		assertEquals(5, nodesIn3Level.size());
		assertEquals(10, nodesIn3Level.get(0).intValue());
		assertEquals(1, nodesIn3Level.get(1).intValue());
		assertEquals(11, nodesIn3Level.get(2).intValue());
		assertEquals(2, nodesIn3Level.get(3).intValue());
		assertEquals(12, nodesIn3Level.get(4).intValue());
		
		System.out.println(nodesIn3Level);
	}

	@Test
	public void bf_search() {
		BinaryTreeNode found = bfTest.search(3, numberRoot);
		assertNotNull(found);
		assertEquals(3, found.getData());
	}

	@Test
	public void bf_search_notFound() {
		BinaryTreeNode foundNA = bfTest.search(100, numberRoot);
		assertNull(foundNA);
	}
}

Execute mvn test -Dtest=BinaryTreeSearchTraverseTest and capture the output here.

Output

-------------------------------------------------------
 T E S T S
-------------------------------------------------------
Running org.jcg.zheng.search.BinaryTreeSearchTraverseTest
bf_search started.
Visited 6 nodes to find the key.

bf_search completed.

bf_search_notFound started.
Visited 16 nodes to find the key.

bf_search_notFound completed.

bf_traverse started.
[10, 1, 11, 2, 12, 3, 13, 4, 14, 5, 15, 6, 16, 7, 8, 9]

bf_traverse completed.

df_search started.

df_search completed.

bf_traverse_limit3 started.
[10, 1, 11, 2, 12]

bf_traverse_limit3 completed.

df_traverse started.
10      1       2       3       4       5       6       7       8       9       11      12      13      14      15      16
df_traverse completed.

Tests run: 6, Failures: 0, Errors: 0, Skipped: 0, Time elapsed: 0.285 sec

Results :

Tests run: 6, Failures: 0, Errors: 0, Skipped: 0

Note:

• line 16: Tree nodes are printed out with BFS.
• line 25: Tree nodes are printed out with max depth of 3.
• line 30: Tree nodes are printed out with DFS.

4.4 Graph BFS algorithm Test

In this step, I will create a GraphBFSTest class which traverses the TreeNode and Vertex via BFS.

GraphBFSTest.java

package org.jcg.zheng.search;

import static org.junit.Assert.assertEquals;
import static org.junit.Assert.assertNotNull;
import static org.junit.Assert.assertNull;

import org.jcg.zheng.data.TreeNode;
import org.jcg.zheng.data.Vertex;
import org.junit.Before;
import org.junit.Rule;
import org.junit.Test;
import org.junit.rules.TestName;

public class GraphBFSTest {

	private TreeNode<String> names;

	private Vertex<String> startVertex;

	private BreadthFirst<String> testClass = new BreadthFirst<>();

	@Rule
	public TestName name = new TestName();

	/**
	 * Build a pentagon with A,B, C, D Vertices
	 */
	private void buildDummyGraph() {
		startVertex = new Vertex<>("A");
		Vertex<String> bVertex = new Vertex<>("B");
		Vertex<String> cVertex = new Vertex<>("C");
		Vertex<String> dVertex = new Vertex<>("D");
		Vertex<String> eVertex = new Vertex<>("E");

		startVertex.connect(bVertex);
		startVertex.connect(eVertex);

		cVertex.connect(bVertex);
		cVertex.connect(dVertex);

		dVertex.connect(cVertex);

	}

	/**
	 * Family Tree: root - Mary child - Zack, Ben - Zack child - Tom
	 */
	private void buildDummyTree() {
		names = TreeNode.of("Mary");
		TreeNode<String> firstChild = names.addChild("Zack");
		names.addChild("Ben");
		firstChild.addChild("Tom");
	}

	@Test
	public void search_Graph() {
		Vertex<String> aVertex = testClass.search("D", startVertex);
		assertNotNull(aVertex);
		assertEquals("D", aVertex.getName());
	}

	@Test
	public void search_Graph_2() {
		Vertex<String> aVertex = testClass.search("C", startVertex);
		assertNotNull(aVertex);
		assertEquals("C", aVertex.getName());
	}

	@Test
	public void search_Tree() {
		TreeNode<String> foundAlex = testClass.search("Zack", names);
		assertEquals("Zack", foundAlex.getData());
	}

	@Test
	public void search_Tree_grandChild() {

		TreeNode<String> foundTom = testClass.search("Tom", names);
		assertEquals("Tom", foundTom.getData());
	}

	@Test
	public void search_Tree_not_found() {
		TreeNode<String> foundNA = testClass.search("NA", names);
		assertNull(foundNA);
	}

	@Before
	public void setup() {
		System.out.println(name.getMethodName() + " start");
		buildDummyTree();
		buildDummyGraph();
	}

	@Test
	public void traverse_Graph() {
		testClass.traverse(startVertex);
	}

	@Test
	public void traverse_Tree() {
		testClass.traverse(names);
	}
}

Execute mvn test -Dtest=GraphBFSTest and capture the output here.

Output

-------------------------------------------------------
 T E S T S
-------------------------------------------------------
Running org.jcg.zheng.search.GraphBFSTest
traverse_Graph start
A       E       B       C       D       traverse_Tree start
Mary    Zack    Ben     Tom     search_Tree_grandChild start
Visited Node:Mary
Visited Node:Zack
Visited Node:Ben
Visited Node:Tom
search_Tree_not_found start
Visited Node:Mary
Visited Node:Zack
Visited Node:Ben
Visited Node:Tom
search_Tree start
Visited Node:Mary
Visited Node:Zack
search_Graph start
Visited Vertex:A
Visited Vertex:B
Visited Vertex:E
Visited Vertex:C
Visited Vertex:D
search_Graph_2 start
Visited Vertex:A
Visited Vertex:B
Visited Vertex:E
Visited Vertex:C
Tests run: 7, Failures: 0, Errors: 0, Skipped: 0, Time elapsed: 0.248 sec

Results :

Tests run: 7, Failures: 0, Errors: 0, Skipped: 0

5. Parameter Test

The time complexity of breadth first search algorithm can be expressed as O (V + E) – V is the number of vertices and E is the number of edges.

In this step, I will try to show the time complexity by drawing a line graph based on the execution time for a different input size.

5.1 Parameter Test Base

In this step, I will create a parameterized test to track the execution time of traversing a Binary Tree with both breadth first search algorithm and DFS methods for input tree sizes of {10, 200, 300, … , 19000, 20000}.

ParameterizedTestBase.java

package org.jcg.zheng.search;

import java.io.FileWriter;
import java.io.IOException;
import java.time.Duration;
import java.time.Instant;
import java.util.Arrays;
import java.util.List;
import java.util.Random;

import org.junit.After;
import org.junit.Before;
import org.junit.Rule;
import org.junit.rules.TestName;

public abstract class ParameterizedTestBase {

	private static final int ROOT_NUMBER = 10000;

	protected static final List<Object[]> TEST_SIZE_PARAMETER = Arrays
			.asList(new Object[][] { { 10 }, { 200 }, { 300 }, { 500 }, { 800 }, { 1000 }, { 2000 }, { 3000 }, { 4000 },
					{ 5000 }, { 6000 }, { 7000 }, { 8000 }, { 9000 }, { 10000 }, { 11000 }, { 12000 }, { 13000 },
					{ 14000 }, { 15000 }, { 16000 }, { 17000 }, { 18000 }, { 19000 }, { 20000 } });

	protected String filename;

	private Instant finishTime;

	@Rule
	public TestName name = new TestName();

	protected int nSize;

	protected TestBinaryTree numberRoot = new TestBinaryTree();
	
	protected int searchingKey;

	protected Random randam = new Random();

	private Instant startTime;

	private void buildBinaryTree(int size) {
		int[] items = new int[size + 1];
		items[0] = ROOT_NUMBER;
		int idx = 1;
		numberRoot.add(ROOT_NUMBER);

		// add lower half
		for (int i = ROOT_NUMBER - 1; i >= (ROOT_NUMBER - size / 2); i--) {
			numberRoot.add(i);
			items[idx++] = i;
		}

		// add higher half
		for (int i = ROOT_NUMBER + 1; i <= (ROOT_NUMBER + size / 2); i++) {
			numberRoot.add(i);
			items[idx++] = i;
		}
		searchingKey = items[randam.nextInt(size)];
	}

	@After
	public void cleanup() {
		finishTime = Instant.now();

		long totalTimeInNs = Duration.between(startTime, finishTime).toNanos();

		System.out.printf("\t%s with nSize =%d completed in %d ns\n", name.getMethodName(), nSize, totalTimeInNs);
		if (totalTimeInNs > 0) {
			String line = nSize + "," + totalTimeInNs + "\n";
			writeFile(filename, line);
		}
	}

	@Before
	public void setup() {
		buildBinaryTree(nSize);
		startTime = Instant.now();
	}

	protected void writeFile(String filename, String content) {
		try {
			FileWriter fw = new FileWriter(filename, true);
			fw.write(content);
			fw.close();
		} catch (IOException ioe) {
			System.err.println("IOException: " + ioe.getMessage());
		}
	}
}

5.2 Traverse Search Test

In this step, I will create a TraverseSearchTest class which will execute the traverse and search methods for a BinaryTreeNode with a different size. It will track the execution time for each input size into a comma separated text file.

TraverseParaTest.java

package org.jcg.zheng.search;

import static org.junit.Assert.assertEquals;
import static org.junit.Assert.assertNotNull;

import java.util.Collection;

import org.jcg.zheng.ConstantValues;
import org.jcg.zheng.data.BinaryTreeNode;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runners.Parameterized;


@RunWith(Parameterized.class)
public class TraverseSearchTest extends ParameterizedTestBase {

	@Parameterized.Parameters
	public static Collection input() {
		return TEST_SIZE_PARAMETER;
	}

	private BreadthFirst<Integer> bfTest = new BreadthFirst<>();

	private DepthFirst dfTest = new DepthFirst();

	public TraverseSearchTest(int nSize) {
		super();
		this.nSize = nSize;
	}

	@Test
	public void traverse_bf_BinaryTree() {
		filename = ConstantValues.BREADTH_FIRST_TRAVERAL_CSV;
		bfTest.traverse(this.numberRoot.getRoot());
	}

	@Test
	public void traverse_df_BinaryTrees() {
		filename = ConstantValues.DEPTH_FIRST_TRAVERSE_CSV;
		dfTest.traverse(this.numberRoot.getRoot());
	}

	@Test
	public void search_bf_BinaryTree() {
		filename = ConstantValues.BREADTH_FIRST_SEARCH_CSV;
		BinaryTreeNode found = bfTest.search(this.searchingKey, this.numberRoot.getRoot());

		assertNotNull(found);
		assertEquals(this.searchingKey, found.getData());
		System.out.println("Found " + this.searchingKey);
	}

	@Test
	public void search_df_BinaryTree() {
		filename = ConstantValues.DEPTH_FIRST_SEARCH_CSV;
		BinaryTreeNode found = dfTest.search(this.searchingKey, this.numberRoot.getRoot());
		
		assertNotNull(found);
		assertEquals(this.searchingKey, found.getData());
		System.out.println("Found " + this.searchingKey);
	}
}

As you can see here, the DFS traverses from the root, and explored all the child nodes for the left node before traversing the right node. If the node is very deep, it will encounter StackOverflowError.

Execute the tests and capture the output. You will see that the DFS encountered StackOverflowError when the tree’s depth reaches 5000.

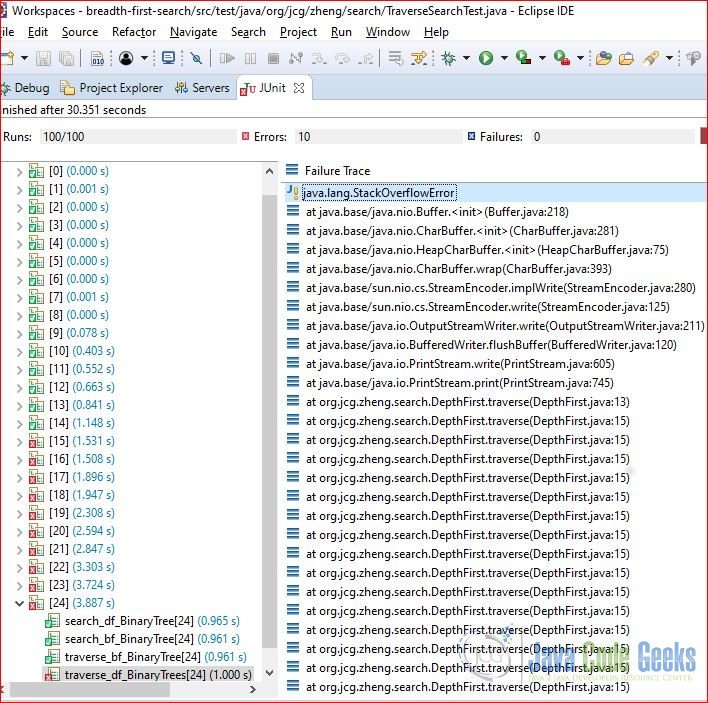
6. Big O Notation

As you seen here, every node/vertex and edge are checked once, so the breadth first search algorithm Big O notation is O (V) for a tree and (V+E) for a graph. V is the number of nodes; E is the number of edges.

We will use the LineGraphChart to display the line graph for the BFS and DFS on a binary tree with different input size.

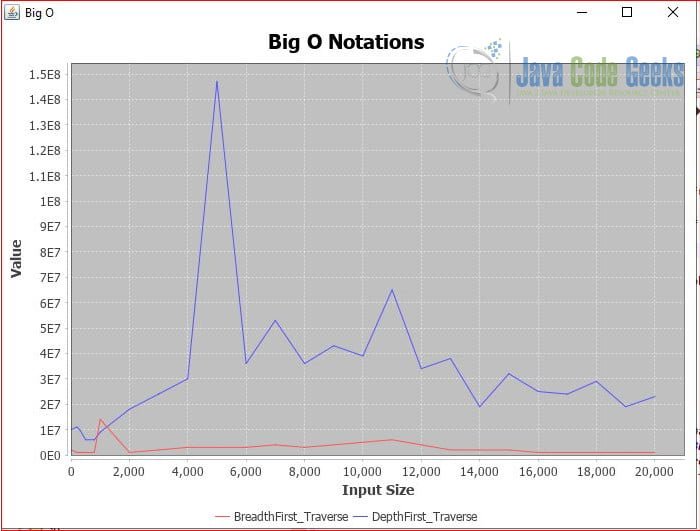
For my test data, the BFS has a better performance than DFS when the tree size and depth increase.

7. Summary

In this example, I demonstrated the BFS algorithm and compared it to the Depth First Search. BFS algorithm can search an item from a Tree or graph data structure.

There are lots of applications which utilizes BFS algorithm:

• Crawlers Search Engine
• Networking to find the shortest path
• GPS Navigation to find the neighboring locations ( restaurants, shopping center, etc)

You can click here for more details.

8. Download the Source Code

Do you want to know how to develop your skillset to become a Java Rockstar?

Subscribe to our newsletter to start Rocking right now!

To get you started we give you our best selling eBooks for FREE!

1. JPA Mini Book

2. JVM Troubleshooting Guide

3. JUnit Tutorial for Unit Testing

4. Java Annotations Tutorial

5. Java Interview Questions

6. Spring Interview Questions

7. Android UI Design

and many more ....

I agree to the Terms and Privacy Policy

Sign up

Thank you!

We will contact you soon.