Bit Masking in Java
1. Introduction
Bit masking is visualizing a number or other data in binary representation. Some bits are set and others are unset where set means true or 1 and unset means false or 0. It allows us to store multiple values inside one numerical variable. You should think of every bit as a separate value instead of thinking of this number as a whole.
2. Bitmasking
Bitmasking is an operation in which we only allow certain bits to pass through while masking other bits. This concept can be more understood by taking an example: Let us say we have a number 10, the binary representation of the number (10)10 is (1010)2. Now let us say we want to find whether the third bit is set or not. To solve this problem we will make use of the bitwise AND operator. So if we need to find whether the third bit is set or not, we are not interested in the other bits. So if we move from the least significant digit to the most (right to left) we are not interested in the first(0), second(1), and fourth(1) bit – so we will be masking these. Masking means that we will apply the bitwise AND operation with 0.
If you have a bit ‘x’ (0/1) and you AND it with 0, you will always get 0. If you have a bit ‘x’ (0/1) and you AND it with 1, you will always get 1 – For example: if x = 0 then 0 & 1 = 0 (which is x), if x = 1 the 1 & 1 = 1 (which is x).
The bits we want to pass through we will bitwise AND with 1. So for the above example, we will bitwise AND 1010 with 0100. Note: Only the third bit from left is 1, the rest are 0s. When you do the bitwise AND if you get a number other than 0 then that particular bit is set, otherwise not set. For our example, we will get 0 (1010 & 0100 = 0000) that means that the third bit was not set.
3. Create Bit Mask
In this section, we will see how to create this bit mask. If we want to check if the kth bit is set or not then we will left shift 1, k-1 times (1 << (k-1)). So if we want to find the mast of the 1st bit we will left shift 1 by 1 – 1 = 0. So it’s 0001. For our example ((10)10) (1010)2 & (0001)2 = (0000)2, so we know that the first bit is not set. Let us check the second(1) bit. To find the mask we will left shift 1 by 1(2 – 1) bit, so we will get 0010. Now if we do 1010 & 0010, we get (0010)2 which is non-zero so we know that the second bit is set.
4. Finding all combinations
In this section, we will see how we can use bit masking to find solutions to some complex problems. Let us say you are given a set S which has three elements S -> {X, Y, Z}. Now we want to find all possible sub-sets of the given set S.
4.1 Recursion
To solve this problem we can see what are the possibilities associated with each element of the set. We find that there are only two possibilities – either you can include that element or you can exclude them. So for X there are two possibilities – I(Included), and E(Excluded), similarly for Y and Z there are two possibilities I, E. So each element has two choices – the total number of choices will be 2 * 2 * 2 = 23 = 8. If we have n elements the number of possibilities will be 2n.
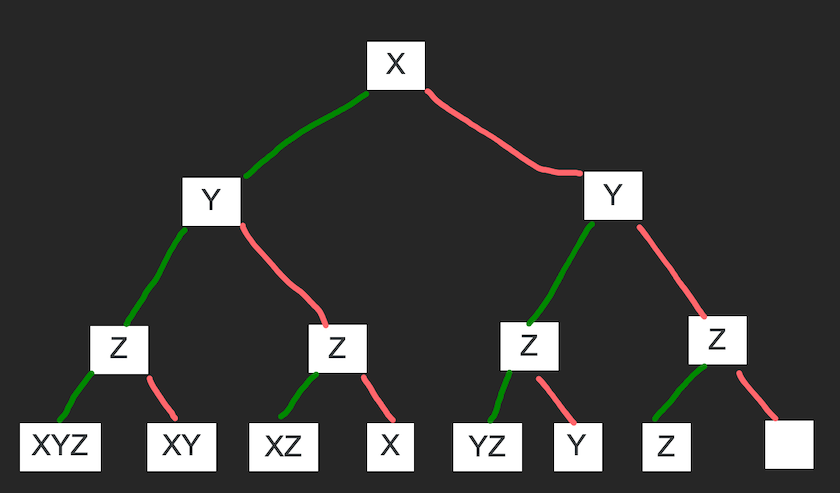
The above diagram represents the recursion tree. When you are at X you have two options – include X or exclude it – green line represents inclusion, and the red represents exclusion. If you follow the tree diagram you will see that the bottom-most line represents the number of possible subsets. The range of a set containing n elements will be from an empty subset to a subset containing all the elements.
4.2 Bit Mask
In this section, we will see how to solve the above problem using a bit mask. We will use 0 to represent exclusion and 1 to represent inclusion. For example, if we have a set containing elements X, Y, Z we can create a mask 100. This will mean that X is included and Y and Z are excluded. So it means {X,Y,Z} -> 100 = {A}. Now if we want to exclude all the elements our mask should be 000, and if we want to include everything it should be 111.
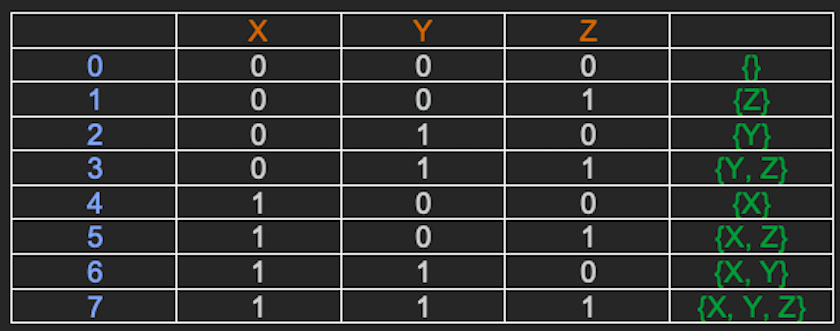
In the above diagram, the second row having 0 as the first element represents the combination where no element is included and the last row represents the combination where all the elements are included. Note that the range will be from 0 to 2n -1, in our case it will be 23 – 1 = 7. So when you are creating the bitmask for the given elements (say n), it includes running a loop from 0 to 2n -1.
5. Conclusion
In this article, we learned about bit masking. We looked at what a bit masking means and how we can create those masks. In the end, we looked at solving the problem using two ways – the first is by using the recursion and the second way is by using the bit mask.


