Big O Notation Java Example
In this post, we feature a comprehensive Big O Notation Java Example.
1. Introduction
Asymptotic notations are used to analyze an algorithm’s running time by identifying its behavior as the input size for the algorithm increases. There are six symbols used to characterize the relative growth rates of functions:
| Symbol | Summary |
| f = Θ(g) | f grows at the same rate as g |
| f = O(g) | f grows no faster than g |
| f = Ω(g) | f grows at least as fast as g |
| f = o(g) | f grows slower than g |
| f = ω(g) | f grows faster than g |
| f ∼ g | f/g approaches 1 |
The algorithm performance can be measured based on the worst-case, best-case, and average-case. Bachmann–Landau notation is an Asymptotic Notation for the worst case or ceiling of growth for a given function. Computer programming uses this notation to classify algorithms according to how their computing time or space requirements grow as the input size grows. Here are the notations ordered from the fastest to slowest:
- O(1) – Constant Time Algorithms. The time is a constant amount of time regardless of the size of n. This is fastest one.
- O(log n) – Logarithmic Time Algorithms – It grows in proportion to the logarithm of the input size.
- O(n) – Linear Time Algorithms – It grows linearly with the input size.
- O(n log n) – N Log N Time Algorithms – It grows in proportion to n log n of the input size.
- O(n^p) – Polynomial Time Algorithms – These algorithms are slower than O(n log n) algorithms.
- O(k^n) – Exponential Time Algorithms – It grows in proportion to some factor exponentiation by the input size.
- O(n!) – Factorial Time Algorithms – It grows to the factorial of the input size. This is the slowest.
In this example, I will create several methods and analyze them with Big O notations: O(1), O(Log n), O(n), and O(n^2).
- Sum an integer series by adding them all. It is O(n) for both time and space complexity.
- Sum an integer series by using formula. It is O(1) for both time and space complexity.
- Find an item from a sorted integer array with binary search algorithm. It is O(Log n) for time complexity and O(1) for space complexity.
- Sort an integer array with insertion sort algorithm. It is O(n^2) for time complexity and O(1) for space complexity.
2. Technologies Used
The example code in this article was built and run using:
- Java 11
- Maven 3.3.9
- Junit 4.12
- Jfreechart 1.5.0
- Eclipse Oxygen
3. Maven Project
In this step, I will create a Maven project which includes four classes to demonstrate these notations. I will use Jfreechart to show the results in a line graph.
3.1 Dependencies
I will include Junit and Jfreechart in the pom.xml.
pom.xml
<project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd"> <modelVersion>4.0.0</modelVersion> <groupId>org.jcg.zheng.demo</groupId> <artifactId>big-o-demo</artifactId> <version>0.0.1-SNAPSHOT</version> <properties> <project.build.sourceEncoding>UTF-8</project.build.sourceEncoding> </properties> <build> <sourceDirectory>src</sourceDirectory> <plugins> <plugin> <artifactId>maven-compiler-plugin</artifactId> <version>3.8.0</version> <configuration> <release>11</release> </configuration> </plugin> </plugins> </build> <dependencies> <dependency> <groupId>junit</groupId> <artifactId>junit</artifactId> <version>4.12</version> </dependency> <dependency> <groupId>org.jfree</groupId> <artifactId>jfreechart</artifactId> <version>1.5.0</version> </dependency> </dependencies> </project>
3.2 FileNameConstants
In this step, I will create a FileNameConstants class to define four text files which store the execution time for each test. The data will be used to draw a line graph later.
FileNameConstants.java
package org.jcg.zheng;
public class FileNameConstants {
public static final String CONSTANT_TIME = "ConstantTime.csv";
public static final String LINEAR_TIME = "LinearTime.csv";
public static final String LOG_TIME = "LogTime.csv";
public static final String QUADRATIC_TIME = "QuadraticTime.csv";
public static final String POLY_TIME = "PolyTime.csv";
}
3.3 LineGraphChart
In this step, I will create a LineGraphChart class which extends from org.jfree.chart.ui.ApplicationFrame. It will draw line graphs for given xy coordinates from the test classes. The xy coordinates are the input size N vs the execution time captured during testing.
LineGraphChart.java
package org.jcg.zheng;
import java.awt.BorderLayout;
import java.awt.Color;
import java.io.File;
import java.io.IOException;
import java.nio.charset.Charset;
import java.nio.file.Files;
import java.util.HashMap;
import java.util.Map;
import javax.swing.JPanel;
import org.jfree.chart.ChartFactory;
import org.jfree.chart.ChartPanel;
import org.jfree.chart.JFreeChart;
import org.jfree.chart.axis.NumberAxis;
import org.jfree.chart.axis.ValueAxis;
import org.jfree.chart.plot.PlotOrientation;
import org.jfree.chart.plot.XYPlot;
import org.jfree.chart.renderer.xy.StandardXYItemRenderer;
import org.jfree.chart.ui.ApplicationFrame;
import org.jfree.data.xy.XYDataset;
import org.jfree.data.xy.XYSeries;
import org.jfree.data.xy.XYSeriesCollection;
public class LineGraphChart extends ApplicationFrame {
private static final long serialVersionUID = 8024827403766653799L;
public static void main(String[] args) {
final LineGraphChart demo = new LineGraphChart("Big O Notations");
demo.pack();
demo.setVisible(true);
}
private XYPlot plot;
public LineGraphChart(String title) {
super(title);
final XYDataset dataset1 = createRandomDataset("O(1)", readCoordinates(FileNameConstants.CONSTANT_TIME));
final JFreeChart chart = ChartFactory.createXYLineChart("Big O Notations", "Input Size", "Value", dataset1,
PlotOrientation.VERTICAL, true, true, false);
chart.setBackgroundPaint(Color.white);
this.plot = chart.getXYPlot();
this.plot.setBackgroundPaint(Color.lightGray);
this.plot.setDomainGridlinePaint(Color.white);
this.plot.setRangeGridlinePaint(Color.white);
final ValueAxis axis = this.plot.getDomainAxis();
axis.setAutoRange(true);
final NumberAxis rangeAxis2 = new NumberAxis("Range Axis 2");
rangeAxis2.setAutoRangeIncludesZero(false);
final JPanel content = new JPanel(new BorderLayout());
final ChartPanel chartPanel = new ChartPanel(chart);
content.add(chartPanel);
chartPanel.setPreferredSize(new java.awt.Dimension(700, 500));
setContentPane(content);
this.plot.setDataset(1, createRandomDataset("O(n)", readCoordinates(FileNameConstants.LINEAR_TIME)));
this.plot.setRenderer(1, new StandardXYItemRenderer());
this.plot.setDataset(2, createRandomDataset("O(logn)", readCoordinates(FileNameConstants.LOG_TIME)));
this.plot.setRenderer(2, new StandardXYItemRenderer());
this.plot.setDataset(3, createRandomDataset("O(n^2)", readCoordinates(FileNameConstants.POLY_TIME)));
this.plot.setRenderer(3, new StandardXYItemRenderer());
}
private XYDataset createRandomDataset(final String label, Map<Long, Long> xyCoordinates) {
XYSeriesCollection dataset = new XYSeriesCollection();
XYSeries series = new XYSeries(label);
xyCoordinates.forEach((k, v) -> {
series.add(k, v);
});
dataset.addSeries(series);
return dataset;
}
private Map<Long, Long> readCoordinates(String filename) {
Map<Long, Long> xyCoordinates = new HashMap<>();
try {
File data = new File(filename);
Files.readAllLines(data.toPath(), Charset.defaultCharset()).forEach(s -> {
System.out.println(s);
String[] values = s.split(",");
xyCoordinates.put(Long.valueOf(values[0]), Long.valueOf(values[1]));
});
} catch (IOException e) {
e.printStackTrace();
}
return xyCoordinates;
}
}
4. Notations
In computer programming, arithmetic operations and accessing array element are considered as one operation. If the algorithm has more operations, then it will take longer execution time.
4.1 O(1) Constant Time
In this step, I will create a ConstantTimeAlgorithm class which sums an integer series from 1 to N. It calculates the sum via a mathematics formula with three operations: one multiplication, one addition and one division. The total number of operations is constant 3 regardless of the input size N. The total memory used is three BigInteger objects.
In this notation, the constant is ignored due to its insignificance. This algorithm has a constant time and space complexity – O(1).
ConstantTimeAlgorithm.java
package org.jcg.zheng;
import java.math.BigInteger;
public class ConstantTimeAlgorithm {
/**
*
* O(1) - Calculate the sum from 1 to N via arithmetic series formula
*/
public BigInteger sumOfArithmeticSeries_via_formula(long n) {
return BigInteger.valueOf(n).multiply(BigInteger.valueOf(n + 1)).divide(BigInteger.valueOf(2));
}
}
4.2 O(n) Linear Time
In this step, I will create a LinearTimeAlgorithm class which sums an integer series from 1 to N. It calculates the sum by adding all the numbers.
The addition operation is inside a for loop, so the total number of operations and total number of objects grow as the input size grows – linear time – O(n).
LinearTimeAlgorithm.java
package org.jcg.zheng;
import java.math.BigInteger;
/**
* Calculate the sum from 1 to N
*
*/
public class LinearTimeAlgorithm {
/**
* O(n) - Calculate the sum from 1 to N via sum all the numbers
*/
public BigInteger sumOfArithmeticSerie_via_add_all(long n) {
BigInteger sum = BigInteger.valueOf(0);
for (long i = 1; i <= n; i++) {
sum = sum.add(BigInteger.valueOf(i));
}
return sum;
}
}
4.3 O(Log n) Logarithmic Time
In this step, I will create a LogarithmicTime class which searches an item from a sorted integer array via binary search algorithm. It has two loops, but the inner loop reduces its size by half for each check. So the total operation is Log(n).
LogarithmicTime.java
package org.jcg.zheng;
public class LogarithmicTimeAlgorithm {
/**
*
* O(log n) - binary search a sorted array. it compares the key value with the
* middle element of the array; if they are unequal, the half in which the key
* cannot be part of is eliminated
*/
public int binarySearchItem(int[] sortedArray, int value) {
int index = -1;
int low = 0;
int high = sortedArray.length;
while (low <= high) {
int mid = (low + high) / 2;
if (sortedArray[mid] < value) {
low = mid + 1;
} else if (sortedArray[mid] > value) {
high = mid - 1;
} else if (sortedArray[mid] == value) {
index = mid;
break;
}
}
return index;
}
}
4.4 O(n^2) Quadratic Time
In this step, I will create a QuadraticAlgorithm class which sorta an integer array via insertation_sort(int[] intArray). The method has two loops.
QuadraticAlgorithm.java
package org.jcg.zheng;
public class QuadraticAlgorithm {
public void insertation_sort(int numberArray[]) {
int n = numberArray.length;
for (int i = 1; i < n; ++i) {
int position = numberArray[i];
int j = i - 1;
while (j >= 0 && numberArray[j] > position) {
numberArray[j + 1] = numberArray[j];
j = j - 1;
}
numberArray[j + 1] = position;
}
}
}
5. JUnit Test
In this step, I will use parameterized Junit tests to capture the methods execution time and memory used when the input size grows. I will use Jfreechart to draw a time and space complexity graph which will demonstrate the constant O(1), linear O(n), and quadratic O(n^2) notations.
5.1 TestBase
In this step, I will create a TestBase class which starts the execute time clock before and after each test. It saves the input size and execution time in a file to later draw them in a graph. It also defines input size array to be used in a parameter tests for these 4 algorithms.
setup()– captures the start timecleanup()– captures the finish time and save the input size to the execution time in a filesetArray()– constructs an integer arraywriteFile()– writes the execution time for each testTEST_SIZE_PARAMETER– is a variable used by theParameterizedtest, so the test can be executed multiple times, one for each parameter. Here I define the input sizes from 10, 200, 300, 500, 800, 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000, 11000, 12000, 13000, 14000, 15000, 16000, 17000, 18000, 19000, to 200000.
TestBase.java
package org.jcg.zheng;
import java.io.FileWriter;
import java.io.IOException;
import java.time.Duration;
import java.time.Instant;
import java.util.Arrays;
import java.util.List;
import java.util.Random;
import org.junit.After;
import org.junit.Before;
import org.junit.Rule;
import org.junit.rules.TestName;
public abstract class TestBase {
@Rule
public TestName name = new TestName();
protected long nSize;
private Instant startTime;
private Instant finishTime;
protected Random randam = new Random();
protected String filename;
protected static final List<Object[]> TEST_SIZE_PARAMETER = Arrays
.asList(new Object[][] { { 10 }, { 200 }, { 300 }, { 500 }, { 800 }, { 1000 }, { 2000 }, { 3000 }, { 4000 },
{ 5000 }, { 6000 }, { 7000 }, { 8000 }, { 9000 }, { 10000 }, { 11000 }, { 12000 }, { 13000 },
{ 14000 }, { 15000 }, { 16000 }, { 17000 }, { 18000 }, { 19000 }, { 20000 } });
@After
public void cleanup() {
finishTime = Instant.now();
long totalTimeInNs = Duration.between(startTime, finishTime).toNanos();
System.out.printf("\t%s with nSize =%d completed in %d ns\n", name.getMethodName(), nSize, totalTimeInNs);
if (totalTimeInNs > 0) {
String line = nSize + "," + totalTimeInNs + "\n";
writeFile(filename, line);
}
}
@Before
public void setup() {
startTime = Instant.now();
}
protected int[] setArray(long arraySize) {
int nSize = (int) arraySize;
int[] items = new int[nSize];
for (int i = 0; i < nSize; i++) {
items[i] = randam.nextInt(10000);
}
return items;
}
private void writeFile(String filename, String content) {
try {
FileWriter fw = new FileWriter(filename, true);
fw.write(content);
fw.close();
} catch (IOException ioe) {
System.err.println("IOException: " + ioe.getMessage());
}
}
}
5.2 ConstantTimeAlgorithmTest
In this step, I will create a ConstantTimeAlgorithmTest to test sumOfArithmeticSeries_via_formula. It extends from TestBase and execute the test repeatedly for various input size.
ConstantTimeAlgorithmTest.java
package org.jcg.zheng;
import java.math.BigInteger;
import java.util.Collection;
import org.junit.Before;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runners.Parameterized;
@RunWith(Parameterized.class)
public class ConstantTimeAlgorithmTest extends TestBase {
@Parameterized.Parameters
public static Collection input() {
return TEST_SIZE_PARAMETER;
}
private ConstantTimeAlgorithm testClass;
public ConstantTimeAlgorithmTest(long nSize) {
super();
this.nSize = nSize;
}
@Before
public void setup() {
testClass = new ConstantTimeAlgorithm();
this.filename = FileNameConstants.CONSTANT_TIME;
super.setup();
}
@Test
public void sumOfArithmeticSeries_via_formula() {
BigInteger total = testClass.sumOfArithmeticSeries_via_formula(nSize);
System.out.println("Sum of 1.." + nSize + " = " + total.longValue());
}
}
Execute it as Junit test and capture the output here.
Output
Sum of 1..10 = 55 sumOfArithmeticSeries_via_formula[0] with nSize =10 completed in 3999500 ns Sum of 1..200 = 20100 sumOfArithmeticSeries_via_formula[1] with nSize =200 completed in 999700 ns Sum of 1..300 = 45150 sumOfArithmeticSeries_via_formula[2] with nSize =300 completed in 0 ns Sum of 1..500 = 125250 sumOfArithmeticSeries_via_formula[3] with nSize =500 completed in 0 ns Sum of 1..800 = 320400 sumOfArithmeticSeries_via_formula[4] with nSize =800 completed in 501300 ns Sum of 1..1000 = 500500 sumOfArithmeticSeries_via_formula[5] with nSize =1000 completed in 0 ns Sum of 1..2000 = 2001000 sumOfArithmeticSeries_via_formula[6] with nSize =2000 completed in 0 ns Sum of 1..3000 = 4501500 sumOfArithmeticSeries_via_formula[7] with nSize =3000 completed in 0 ns Sum of 1..4000 = 8002000 sumOfArithmeticSeries_via_formula[8] with nSize =4000 completed in 1025900 ns Sum of 1..5000 = 12502500 sumOfArithmeticSeries_via_formula[9] with nSize =5000 completed in 0 ns Sum of 1..6000 = 18003000 sumOfArithmeticSeries_via_formula[10] with nSize =6000 completed in 0 ns Sum of 1..7000 = 24503500 sumOfArithmeticSeries_via_formula[11] with nSize =7000 completed in 0 ns Sum of 1..8000 = 32004000 sumOfArithmeticSeries_via_formula[12] with nSize =8000 completed in 0 ns Sum of 1..9000 = 40504500 sumOfArithmeticSeries_via_formula[13] with nSize =9000 completed in 0 ns Sum of 1..10000 = 50005000 sumOfArithmeticSeries_via_formula[14] with nSize =10000 completed in 0 ns Sum of 1..11000 = 60505500 sumOfArithmeticSeries_via_formula[15] with nSize =11000 completed in 3999500 ns Sum of 1..12000 = 72006000 sumOfArithmeticSeries_via_formula[16] with nSize =12000 completed in 996800 ns Sum of 1..13000 = 84506500 sumOfArithmeticSeries_via_formula[17] with nSize =13000 completed in 0 ns Sum of 1..14000 = 98007000 sumOfArithmeticSeries_via_formula[18] with nSize =14000 completed in 0 ns Sum of 1..15000 = 112507500 sumOfArithmeticSeries_via_formula[19] with nSize =15000 completed in 0 ns Sum of 1..16000 = 128008000 sumOfArithmeticSeries_via_formula[20] with nSize =16000 completed in 999700 ns Sum of 1..17000 = 144508500 sumOfArithmeticSeries_via_formula[21] with nSize =17000 completed in 1000100 ns Sum of 1..18000 = 162009000 sumOfArithmeticSeries_via_formula[22] with nSize =18000 completed in 0 ns Sum of 1..19000 = 180509500 sumOfArithmeticSeries_via_formula[23] with nSize =19000 completed in 0 ns Sum of 1..20000 = 200010000 sumOfArithmeticSeries_via_formula[24] with nSize =20000 completed in 999600 ns
5.3 LinerTimeAlgorithmTest
In this step, I will create a LinearTimeAlgorithmTest to test sumOfArithmeticSeries_via_add_all. It extends from TestBase.
LinearTimeAlgorithmTest.java
package org.jcg.zheng;
import java.math.BigInteger;
import java.util.Collection;
import org.junit.Before;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runners.Parameterized;
@RunWith(Parameterized.class)
public class LinearTimeAlgorithmTest extends TestBase {
@Parameterized.Parameters
public static Collection input() {
return TEST_SIZE_PARAMETER;
}
private LinearTimeAlgorithm testClass;
public LinearTimeAlgorithmTest(long nSize) {
super();
this.nSize = nSize;
}
@Before
public void setup() {
testClass = new LinearTimeAlgorithm();
this.filename = FileNameConstants.LINEAR_TIME;
super.setup();
}
@Test
public void sumOfArithmeticSeries_via_add_all() {
BigInteger total = testClass.sumOfArithmeticSerie_via_add_all(nSize);
System.out.println("Sum of 1.." + nSize + " =" + total.longValue());
}
}
Execute it as Junit test and capture the output here.
Output
Sum of 1..10 =55 sumOfArithmeticSeries_via_add_all[0] with nSize =10 completed in 4002400 ns Sum of 1..200 =20100 sumOfArithmeticSeries_via_add_all[1] with nSize =200 completed in 0 ns Sum of 1..300 =45150 sumOfArithmeticSeries_via_add_all[2] with nSize =300 completed in 1999800 ns Sum of 1..500 =125250 sumOfArithmeticSeries_via_add_all[3] with nSize =500 completed in 1002100 ns Sum of 1..800 =320400 sumOfArithmeticSeries_via_add_all[4] with nSize =800 completed in 999300 ns Sum of 1..1000 =500500 sumOfArithmeticSeries_via_add_all[5] with nSize =1000 completed in 998900 ns Sum of 1..2000 =2001000 sumOfArithmeticSeries_via_add_all[6] with nSize =2000 completed in 1995300 ns Sum of 1..3000 =4501500 sumOfArithmeticSeries_via_add_all[7] with nSize =3000 completed in 999700 ns Sum of 1..4000 =8002000 sumOfArithmeticSeries_via_add_all[8] with nSize =4000 completed in 1998500 ns Sum of 1..5000 =12502500 sumOfArithmeticSeries_via_add_all[9] with nSize =5000 completed in 1998100 ns Sum of 1..6000 =18003000 sumOfArithmeticSeries_via_add_all[10] with nSize =6000 completed in 2999000 ns Sum of 1..7000 =24503500 sumOfArithmeticSeries_via_add_all[11] with nSize =7000 completed in 1496400 ns Sum of 1..8000 =32004000 sumOfArithmeticSeries_via_add_all[12] with nSize =8000 completed in 1997300 ns Sum of 1..9000 =40504500 sumOfArithmeticSeries_via_add_all[13] with nSize =9000 completed in 1497600 ns Sum of 1..10000 =50005000 sumOfArithmeticSeries_via_add_all[14] with nSize =10000 completed in 1998100 ns Sum of 1..11000 =60505500 sumOfArithmeticSeries_via_add_all[15] with nSize =11000 completed in 3996300 ns Sum of 1..12000 =72006000 sumOfArithmeticSeries_via_add_all[16] with nSize =12000 completed in 8997500 ns Sum of 1..13000 =84506500 sumOfArithmeticSeries_via_add_all[17] with nSize =13000 completed in 997200 ns Sum of 1..14000 =98007000 sumOfArithmeticSeries_via_add_all[18] with nSize =14000 completed in 999700 ns Sum of 1..15000 =112507500 sumOfArithmeticSeries_via_add_all[19] with nSize =15000 completed in 1005500 ns Sum of 1..16000 =128008000 sumOfArithmeticSeries_via_add_all[20] with nSize =16000 completed in 1003800 ns Sum of 1..17000 =144508500 sumOfArithmeticSeries_via_add_all[21] with nSize =17000 completed in 2998600 ns Sum of 1..18000 =162009000 sumOfArithmeticSeries_via_add_all[22] with nSize =18000 completed in 1001300 ns Sum of 1..19000 =180509500 sumOfArithmeticSeries_via_add_all[23] with nSize =19000 completed in 3999100 ns Sum of 1..20000 =200010000 sumOfArithmeticSeries_via_add_all[24] with nSize =20000 completed in 3999500 ns
5.4 Logarithmic Time O (log n)
In this step, I will create a LogarithmicTimeTest which extends from TestBase. It tests binarySearch repeatedly for various input size.
LoogatithmicTimeTest.java
package org.jcg.zheng;
import java.util.Arrays;
import java.util.Collection;
import org.junit.Before;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runners.Parameterized;
@RunWith(Parameterized.class)
public class LogarithmicTimeAlgorithmTest extends TestBase {
@Parameterized.Parameters
public static Collection input() {
return TEST_SIZE_PARAMETER;
}
private int[] integerArray;
private int searchingItem;
private LogarithmicTimeAlgorithm testClass = new LogarithmicTimeAlgorithm();
public LogarithmicTimeAlgorithmTest(long nSize) {
super();
this.nSize = nSize;
}
@Before
public void setup() {
integerArray = setArray(this.nSize);
Arrays.sort(integerArray);
int intSearchItemPo = randam.nextInt((int) this.nSize);
searchingItem = integerArray[intSearchItemPo];
this.filename = FileNameConstants.LOG_TIME;
super.setup();
}
@Test
public void binarySearchItem() {
int foundKey = testClass.binarySearchItem(integerArray, searchingItem);
System.out.printf("Searching %d in array[%d], found at position %d\n", searchingItem, integerArray.length,
foundKey);
}
}
Execute binarySearchItem as Junit test and capture the output here.
Output
Searching 3965 in array[10], found at position 4 binarySearchItem[0] with nSize =10 completed in 2501900 ns Searching 9319 in array[200], found at position 184 binarySearchItem[1] with nSize =200 completed in 1001800 ns Searching 1609 in array[300], found at position 51 binarySearchItem[2] with nSize =300 completed in 1501400 ns Searching 6749 in array[500], found at position 334 binarySearchItem[3] with nSize =500 completed in 499200 ns Searching 8917 in array[800], found at position 715 binarySearchItem[4] with nSize =800 completed in 4002000 ns Searching 3590 in array[1000], found at position 368 binarySearchItem[5] with nSize =1000 completed in 500900 ns Searching 4360 in array[2000], found at position 891 binarySearchItem[6] with nSize =2000 completed in 499200 ns Searching 7396 in array[3000], found at position 2236 binarySearchItem[7] with nSize =3000 completed in 2500600 ns Searching 7483 in array[4000], found at position 3003 binarySearchItem[8] with nSize =4000 completed in 1500100 ns Searching 449 in array[5000], found at position 210 binarySearchItem[9] with nSize =5000 completed in 999700 ns Searching 3587 in array[6000], found at position 2131 binarySearchItem[10] with nSize =6000 completed in 1002100 ns Searching 8680 in array[7000], found at position 6031 binarySearchItem[11] with nSize =7000 completed in 1999800 ns Searching 5953 in array[8000], found at position 4774 binarySearchItem[12] with nSize =8000 completed in 0 ns Searching 9867 in array[9000], found at position 8877 binarySearchItem[13] with nSize =9000 completed in 1001400 ns Searching 2846 in array[10000], found at position 2781 binarySearchItem[14] with nSize =10000 completed in 996800 ns Searching 7826 in array[11000], found at position 8590 binarySearchItem[15] with nSize =11000 completed in 5001700 ns Searching 5265 in array[12000], found at position 6322 binarySearchItem[16] with nSize =12000 completed in 1002200 ns Searching 8071 in array[13000], found at position 10542 binarySearchItem[17] with nSize =13000 completed in 1997700 ns Searching 7123 in array[14000], found at position 9953 binarySearchItem[18] with nSize =14000 completed in 1499300 ns Searching 8053 in array[15000], found at position 12098 binarySearchItem[19] with nSize =15000 completed in 1001700 ns Searching 4520 in array[16000], found at position 7239 binarySearchItem[20] with nSize =16000 completed in 0 ns Searching 2803 in array[17000], found at position 4817 binarySearchItem[21] with nSize =17000 completed in 0 ns Searching 8273 in array[18000], found at position 14908 binarySearchItem[22] with nSize =18000 completed in 1000500 ns Searching 7114 in array[19000], found at position 13430 binarySearchItem[23] with nSize =19000 completed in 1000500 ns Searching 9817 in array[20000], found at position 19653 binarySearchItem[24] with nSize =20000 completed in 0 ns
5.5 Quadratic Time O(n^2)
In this step, I will create a QuadraticAlgorithmTest which extends from TestBase.
QuadraticTimeAlgorithmTest.java
package org.jcg.zheng;
import java.util.Collection;
import org.junit.Before;
import org.junit.Test;
import org.junit.runner.RunWith;
import org.junit.runners.Parameterized;
@RunWith(Parameterized.class)
public class QuadraticAlgorithmTest extends TestBase {
@Parameterized.Parameters
public static Collection input() {
return TEST_SIZE_PARAMETER;
}
private int[] integerArray;
private QuadraticAlgorithm testClass;
public QuadraticAlgorithmTest(int nSize) {
super();
this.nSize = nSize;
}
@Test
public void insertation_sort() {
testClass.insertation_sort(integerArray);
}
@Before
public void setup() {
testClass = new QuadraticAlgorithm();
integerArray = setArray(this.nSize);
this.filename = FileNameConstants.POLY_TIME;
super.setup();
}
}
Execute insertation_sort as Junit test and capture the output here.
Output
insertation_sort[0] with nSize =10 completed in 0 ns insertation_sort[1] with nSize =200 completed in 999300 ns insertation_sort[2] with nSize =300 completed in 1500100 ns insertation_sort[3] with nSize =500 completed in 2998200 ns insertation_sort[4] with nSize =800 completed in 4497500 ns insertation_sort[5] with nSize =1000 completed in 11499700 ns insertation_sort[6] with nSize =2000 completed in 1501400 ns insertation_sort[7] with nSize =3000 completed in 2000200 ns insertation_sort[8] with nSize =4000 completed in 5500000 ns insertation_sort[9] with nSize =5000 completed in 5498400 ns insertation_sort[10] with nSize =6000 completed in 10500400 ns insertation_sort[11] with nSize =7000 completed in 12502300 ns insertation_sort[12] with nSize =8000 completed in 16000100 ns insertation_sort[13] with nSize =9000 completed in 20497600 ns insertation_sort[14] with nSize =10000 completed in 27997800 ns insertation_sort[15] with nSize =11000 completed in 33000300 ns insertation_sort[16] with nSize =12000 completed in 25995200 ns insertation_sort[17] with nSize =13000 completed in 40053400 ns insertation_sort[18] with nSize =14000 completed in 61015800 ns insertation_sort[19] with nSize =15000 completed in 44512800 ns insertation_sort[20] with nSize =16000 completed in 41013700 ns insertation_sort[21] with nSize =17000 completed in 44513200 ns insertation_sort[22] with nSize =18000 completed in 56512500 ns insertation_sort[23] with nSize =19000 completed in 60998100 ns insertation_sort[24] with nSize =20000 completed in 84023900 ns
5.6 Big O Test Suite
In this step, I will create a BigOTestSuite class which includes ConstantTimeAlgorithmTest, LinearTimeAlgorithmTest, LogarithmicTimeAlgorithmTest, and QuadraticAlgorithmTest class. It will draw a graph to show the execution time relates to the input size for each algorithm.
BigOTestSuite.java
package org.jcg.zheng;
import org.junit.AfterClass;
import org.junit.runner.RunWith;
import org.junit.runners.Suite;
import org.junit.runners.Suite.SuiteClasses;
@RunWith(Suite.class)
@SuiteClasses({ ConstantTimeAlgorithmTest.class, LinearTimeAlgorithmTest.class, LogarithmicTimeAlgorithmTest.class,
QuadraticAlgorithmTest.class })
public class BigOTestSuite {
@AfterClass
public static void tearDown() {
LineGraphChart xyChart = new LineGraphChart("Big O Notations");
xyChart.setVisible(true);
xyChart.pack();
System.out.println("DONE");
}
}
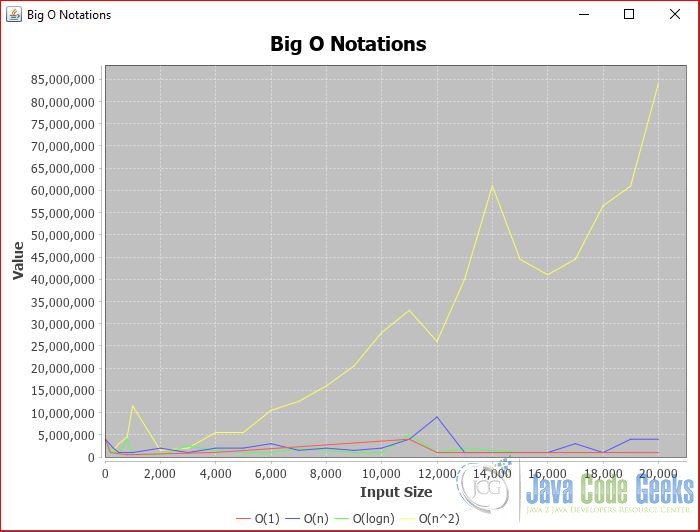
At the end of test, it will draw a line graph with 4 lines with different color:
- O(1) – red line, it is an almost parallel line to the X axis.
- O(log n) – green line, it grows slower than the linear line.
- O(n) – blue line, it grows a little faster than the logarithm line.
- O(n^2) – yellow line, it grows quickly when the input size grows.
6. Big O Notation Java Example – Summary
In this example, we explained what this notation is and created four methods and explained their time and space efficiency when the input size grows.
As you seen, the O(n^2) grows quickly when the input size grows. Developers should be careful with an algorithm in which this notation is slower than O(n^2). Click here for a completed list of this analysis for the most known sorting algorithms by Eric Rowel.
As a Java developer, we should analyze the algorithm to make sure it meets the business requirements and potential growth.
7. Download the Source Code
This Big O Notation Java example consists of a Maven project which shows time and space complexity analysis via these notations.
You can download the full source code of this example here: Big O Notation Java Example


