Master Theorem
1. Introduction
An algorithm is a well-defined instruction set designed to solve a particular problem for the given input data sets
Master theorem refers to the fact that you can solve a problem in a divide-and-conquer way to provide an asymptotic analysis. We can use this in the analysis of many divide and conquer algorithms.
This algorithm was firstly presented by Jon Bentley, Dorothea Haken, and James B. Saxe in 1980, where it was presented as a unifying method for solving recurrence problems. Cormen, Leiserson, Rivest, and Stein introduce this concept in their book: Introduction to Algorithms where became famous under the name: master theorem.
2. What is Master Theorem?
This method is used to solve recurrence relations. The formula describing this method is:
T(n) = a T(n/b) + f(n)
The meaning of each parameter, where a>= 1, b >1:
- n – size of input
- a – number of subproblems in the recursion
- n/b – size of each subproblem (assume that all subproblems have the same size)
- f(n) – time to create the subproblems and combine their results in the above procedure
Master Theorem is a very useful and when it comes to design and analysis for divide and conquer technique. Above all mentioned, the master theorem provides the solution in asymptotic terms (time complexity) for recurrence relations. The recurrence relation is dependent on the previous runs.
3. Solved Examples with Master Theorem
Examples solved with master theorem.
3.1. Case Example 1
T(n) = 8T(n/2) + n2
Where the parameters are (taking into consideration the base formula):
a = 8; b = 2; f(n) = n2
f(n) = O(nc); c= 2
logb a = log2 8 = 3 > c;
T(n) = O (nlogb a) = O(n3)
3.2. Case Example 2
T(n) = 2T(n/2) + n
a = 2, b = 2, c = 1, f(n) = n;
f(n) = O(nc + logkn), where c= 1; k = 0;
logb a = log2 2 = 1. What we can see is that c = logb a;
T(n) = O(nlogb a logk+1 n) = O(n1 log1n) = O (n log n);
Thus the given recurrence relation T(n) was in O(n log n).
3.3. Case Example 3
T(n) = 2T(n/2) + n2
a = 2, b = 2, f(n) = n2
f(n) = Omega(nc), where c = 2;
logb a = log2 2 = 1, and therefore, yes, c > logb a where, T(n) = O(f(n)) = O (n2).
The recurrence relation T(n) was in O(n2) and compiles with f(n) of the original formula.
More information with practice problems you can find here.
4. Master Theorem Limitations
Likewise other algorithms the Master Theorem has some limitations that are not efficient and cannot be used in some cases.
The limitations are:
- T(n) is not monotone
T(n) = T(n/2) + n (2 – cos n) => regularity violation. - f(n) is not a polynomial
T(n) = 2 T(n/2) + n/ log n => non-polynomial difference f(n) and nlogb n. - a is not a constant
T(n) = 2n T(n/2) + nn => a is not a constant (subproblem size should be fixed). - this method cannot be used if f(n), the combination/merging time is not positive. f(n) should be positive.
T(n) = 64T(n/8) – n2 log n => f(n) combination time, which is not positive. - the value of a should be constant and always greater than 1.
T(n) = 0.5T(n/2) + n => a < 1 cannot have less than 1 problem. - the value of b should be greater than 1.
5. Time complexity
Time complexity of an algorithm is the efficiency that the given set of instructions can solve the problem. In other words, time complexity is a concept in Computer Science that deals with quantification of the amount of time taken by the set of code to process or run as a function for the given input set.
The most common time complexity in computer science are:
- O(1) – constant. This is when accessing a specific element from an array.
- O(n) – linear. Looping through an array of elements.
- O(log n) – logarithmic. Finding an element in a sorted array.
- O(n2) – quadratic. Looping for in for.
- O(2n) – exponential. Double recursion in Fibonacci.
For the most important algorithms the time complexity calculated with master theorem is:
- Binary search. T(n) = T(n/2) + O(1). With time complexity of: O(log n)
- Binary tree transversal. T(n) = 2T(n/2) + O(1). With time complexity of: O(n).
- Optimal sorted matrix sort. T(n) = 2T(n/2) + O(log n). With time complexity of: O(n)
- Merge sort. T(n) = 2T(n/2) + O(n). With time complexity of: O(n log n).
The time complexity grows as the input grows. Best practice time complexity are below O(n), which are: O(log n) or O(1).
6. Java examples
For instance, let’s write a simple java example for the master theorem. We will show you a Java example to prove the Master Theorem with Merge Sort.
/**
* Merge and sort the array
*
* @param inputArray the given input array to sort
* @param beginning the beginning of the array
* @param end the end index of the array
*/
private static void mergeAndSort(int[] inputArray, int beginning, int end) {
if(beginning < end) {
int midOfArray = (beginning + end) / 2;
mergeAndSort(inputArray, beginning, midOfArray);
mergeAndSort(inputArray, midOfArray + 1, end);
merge(inputArray, beginning, midOfArray, end);
}
}
public static void main(String[] args) {
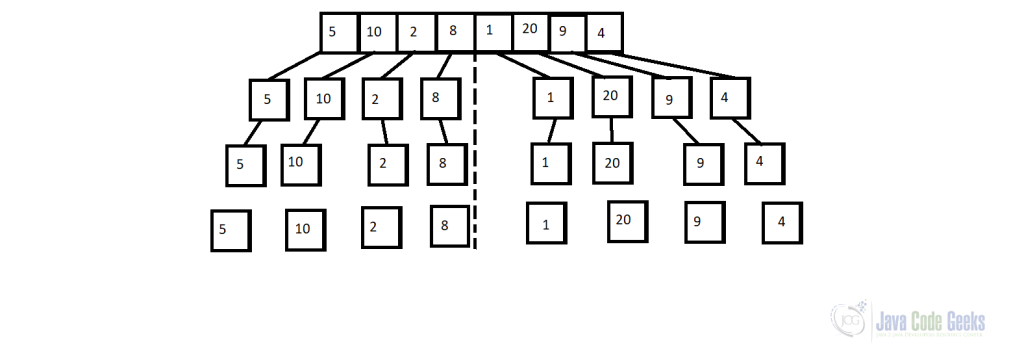
final int[] customArray = new int[]{5, 10, 2, 8, 1, 20, 9, 4};
mergeAndSort(customArray, 0, customArray.length - 1);
System.out.println("The sorted array is: " + Arrays.toString(customArray));
}
The output of the above snippet code:
The sorted array is: [1, 2, 4, 5, 8, 9, 10, 20]
Process finished with exit code 0
If you want to run this class from cmd line you can execute this command in the root of the project (that you downloaded from the download section):
java src/MergeSort.java
I just added just a part of the code. If you want to see the full code please download it from the below section.
7. Final note
As a last note about this article, I could say that this theorem can be used in many day-to-day tasks to solve recurrence problems.
To sum up, the ideas presented in this article were to introduce you to the concept of the Master Theorem with a bit of knowledge about how it starts and the person who invented this concept.
Likewise in other articles, we have some examples with this theorem to better understand the concept.
You can download the full source code for this article here: Master Theorem


